题目内容
已知命题p:0<a<3,命题q:对数函数y=log2a-3x在(0,+∞)上是递增函数,如果命题“¬p或q”是假命题,那么实数a的取值范围是 .
考点:复合命题的真假
专题:阅读型,简易逻辑
分析:根据对数函数的单调性求得命题q为真时a的范围,再根据复合命题真值表得:如果命题“¬p或q”是假命题,
则命题¬p与命题q都是假命题,由此可得a的范围.
则命题¬p与命题q都是假命题,由此可得a的范围.
解答:
解:由函数y=log2a-3x在(0,+∞)上是递增函数得:2a-3>1⇒a>2,
∴命题q为真时,a>2;
由复合命题真值表知:如果命题“¬p或q”是假命题,则命题¬p与命题q都是假命题,
¬p为假命题,0<a<3;
命题q为假命题,a≤2,
∴命题“¬p或q”是假命题的a的范围是0<a≤2.
故答案为:(0,2].
∴命题q为真时,a>2;
由复合命题真值表知:如果命题“¬p或q”是假命题,则命题¬p与命题q都是假命题,
¬p为假命题,0<a<3;
命题q为假命题,a≤2,
∴命题“¬p或q”是假命题的a的范围是0<a≤2.
故答案为:(0,2].
点评:本题借助复合命题的真假判定,考查了对数函数的单调性,熟练掌握对数函数的单调性及复合命题的真值表是解题的关键.

练习册系列答案
相关题目
双曲线x2-
=1的右焦点到准线的距离为( )
| y2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
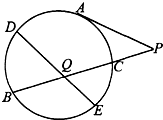 如图,PA为圆的切线,切点为A,割线PCB与圆相交于B、C两点,弦DE经过弦BC的中点Q,若AP=3
如图,PA为圆的切线,切点为A,割线PCB与圆相交于B、C两点,弦DE经过弦BC的中点Q,若AP=3