题目内容
15.设等比数列{an}的各项均为正数,其前n项和为Sn,若a1=1,a3=4.(1)若Sk=63,求k的值;
(2)设bn=log2an,证明数列{bn}是等差数列;
(3)设cn=(-1)nbn,求T=|c1|+|c2|+|c3|+…+|cn|.
分析 (1)利用等比数列的通项公式与求和公式即可得出.
(2)an=2n-1,bn=log2an=n-1,作差即可证明.
(3)cn=(-1)nbn=(-1)n(n-1),|cn|=n-1.再利用等差数列的求和公式即可得出.
解答 解:(1)设等比数列{an}的公比为q,由已知a1=1,a3=4,得q2=$\frac{{a}_{3}}{{a}_{1}}$=4.
又{an}的各项均为正数,∴q=2.-------------------------------------------(2分)
而Sk=$\frac{1-{2}^{k}}{1-2}$=63,∴2k-1=63,解得k=6.-------------------------(4分)
(2)证明:an=2n-1,---------------------------------------------(5分)
bn=log2an=n-1,-----(6分)
bn-bn-1=n-1-(n-1)+1=1.------------------------------(8分)
故数列{bn}是公差为1,首项为0的等差数列.-------------------(9分)
(3)cn=(-1)nbn=(-1)n(n-1).------------------------(11分)
|cn|=n-1.
∴T=|c1|+|c2|+|c3|+…+|cn|=0+1+2+…+(n-1)=$\frac{n(n-1)}{2}$.…(14分)
点评 本题考查了等差数列与等比数列的通项公式与求和公式、对数的运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
3.设函数f(x)=$\frac{1}{2}$x2-9lnx在区间[a-1,a+1]上单调递减,则实数a的取值范围是( )
| A. | (1,2] | B. | [4,+∞) | C. | (-∞,2] | D. | (0,3] |
10.如图茎叶图中有8个数字,茎为十位数,叶为个位数,则这组数据的中位数是( )


| A. | 91 | B. | 92 | C. | 91.5 | D. | 80.25 |
20.在△ABC中,点D满足$\overrightarrow{BC}$=3$\overrightarrow{BD}$,则( )
| A. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | B. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AC}$ | C. | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$ | D. | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$-$\frac{1}{3}$$\overrightarrow{AC}$ |
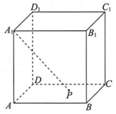 如图,正方体ABCD-A1B1C1D1的棱长为2,点P在正方形ABCD的边界及其内部运动.平面区域W由所有满足A1P≥$\sqrt{5}$的点P组成,则W的面积是$\frac{π}{4}$.
如图,正方体ABCD-A1B1C1D1的棱长为2,点P在正方形ABCD的边界及其内部运动.平面区域W由所有满足A1P≥$\sqrt{5}$的点P组成,则W的面积是$\frac{π}{4}$.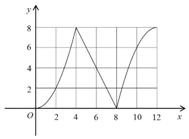 如图,函数f(x)的图象经过(0,0),(4,8),(8,0),(12,8)四个点,试用“>,=,<”填空:
如图,函数f(x)的图象经过(0,0),(4,8),(8,0),(12,8)四个点,试用“>,=,<”填空: