题目内容
5.数列{an}中,a1=2,an+1=$\frac{{a}_{n}}{{a}_{n}+1}$,则a2017=$\frac{2}{4033}$.分析 求关系式的倒数,得到新数列是等差数列,然后求解通项公式,求解即可.
解答 解:数列{an}中,a1=2,an+1=$\frac{{a}_{n}}{{a}_{n}+1}$,
可得$\frac{1}{{a}_{n+1}}=1+\frac{1}{{a}_{n}}$,所以{$\frac{1}{{a}_{n}}$}是以$\frac{1}{2}$为首项,1为公差的等差数列,
所以$\frac{1}{{a}_{n}}=\frac{1}{2}+n-1$,
可得an=$\frac{2}{2n-1}$,
则a2017=$\frac{2}{4033}$.
故答案为:$\frac{2}{4033}$.
点评 本题考查数列的递推关系式的应用,数列的通项公式的求法,考查计算能力.

练习册系列答案
相关题目
1.若集合A={-2,-1,0,1,2},集合B={x|x(x+3)<0},则A∩B等于( )
| A. | {-1,0,1,2} | B. | {-2,-1} | C. | {1,2} | D. | {0,1,2} |
17.为了了解青少年的肥胖情况是否与常喝碳酸饮料有关,现对30名青少年进行调查,得到如下列联表:
已知从这30名青少年中随机抽取1名,抽到肥胖青少年的概率为$\frac{4}{15}$.
(1)请将上面的列联表补充完整.
(2)是否有99.5%的把握认为青少年的肥胖与常喝碳酸饮料有关?
(3)若这30名青少年中,常喝碳酸饮料且肥胖的有2名女生,则从常喝碳酸饮料且肥胖的青少年中随机抽取2名,恰好抽到一男一女的概率是多少?
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a-b)(c+d)(a-c)(b+d)}$,其中n=a+b+c+d)
| 常喝 | 不常喝 | 总计 | |
| 肥胖 | 2 | ||
| 不肥胖 | 18 | ||
| 总计 | 30 |
(1)请将上面的列联表补充完整.
(2)是否有99.5%的把握认为青少年的肥胖与常喝碳酸饮料有关?
(3)若这30名青少年中,常喝碳酸饮料且肥胖的有2名女生,则从常喝碳酸饮料且肥胖的青少年中随机抽取2名,恰好抽到一男一女的概率是多少?
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a-b)(c+d)(a-c)(b+d)}$,其中n=a+b+c+d)
| p(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
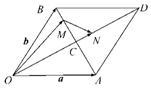 如图,平行四边形OADB的对角线OD、AB相交于点C,线段BC上有一点M满足BC=3BM,线段CD上有一点N满足CD=3CN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,试用a,b表示$\overrightarrow{OM}$,$\overrightarrow{ON}$,$\overrightarrow{MN}$.
如图,平行四边形OADB的对角线OD、AB相交于点C,线段BC上有一点M满足BC=3BM,线段CD上有一点N满足CD=3CN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,试用a,b表示$\overrightarrow{OM}$,$\overrightarrow{ON}$,$\overrightarrow{MN}$.