题目内容
已知函数f(x)=
.
(1)求f(f(
))的值;
(2)画出函数的图象,并根据图象写出函数的值域和单调区间;
(3)若函数g(x)=f(x)-m有四个不同零点,求m的取值范围,并求出这四个零点的和.
|
(1)求f(f(
| 5 |
| 2 |
(2)画出函数的图象,并根据图象写出函数的值域和单调区间;
(3)若函数g(x)=f(x)-m有四个不同零点,求m的取值范围,并求出这四个零点的和.
考点:分段函数的应用
专题:函数的性质及应用
分析:(1)利用分段函数,直接代入求值即可.
(2)根据分段函数,作出函数的图象,结合图象确定函数的值域和单调区间.
(3)利用方程f(x)=m有四个根,建立条件关系,求实数m的取值范围.
(2)根据分段函数,作出函数的图象,结合图象确定函数的值域和单调区间.
(3)利用方程f(x)=m有四个根,建立条件关系,求实数m的取值范围.
解答:
解:(1)f(
)=-
,∴f(f(
))=f(-
)=
.
(2)在平面直角坐标系内画出此分段函数的图象为:

由图象可知,函数的值域是(-∞,1],
单调增区间(-∞,-1]和[0,1],
减区间[-1,0]和[1,+∞).
(3)若函数g(x)=f(x)-m有四个不同零点,∴方程f(x)=m有四个根,
∴根据图象可得实数m的取值范围是0<m<1,
由图象判断f(x)是偶函数,所以这四个根的和是0.
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
(2)在平面直角坐标系内画出此分段函数的图象为:

由图象可知,函数的值域是(-∞,1],
单调增区间(-∞,-1]和[0,1],
减区间[-1,0]和[1,+∞).
(3)若函数g(x)=f(x)-m有四个不同零点,∴方程f(x)=m有四个根,
∴根据图象可得实数m的取值范围是0<m<1,
由图象判断f(x)是偶函数,所以这四个根的和是0.
点评:本题主要考查分段函数的图象和性质,以及函数图象交点问题的应用,利用数形结合是解决此类问题的基本方法.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
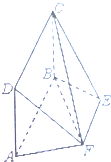 如图,四边形ABCD为矩形,ABEF为梯形,AD=
如图,四边形ABCD为矩形,ABEF为梯形,AD=| 3 |
(1)求证:平面DAF⊥平面CBF;
(2)求二面角D-FC-B的正弦值.
在同一坐标系下函数y=-x+a和y=ax图象可能是( )
A、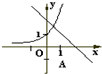 |
B、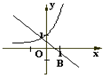 |
C、 |
D、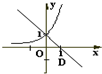 |
设
、
都是非零向量,下列四个条件中,一定能使
+
=
成立的是( )
| a |
| b |
| ||
| |a| |
| ||
| |b| |
| 0 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知集合M={x||x+2|+|x-1|≤5},N={x|a<x<6},且M∩N=(-1,b],则b-a=( )
| A、-3 | B、3 | C、C-1 | D、7 |
已知两点A(-2,1),B(1,5),点C是圆(x-1)2+(y+2)2=9上的动点,则△ABC面积的最大值为( )
| A、36 | B、18 | C、16 | D、8 |