题目内容
已知三个实数a,b,c,当c>0时满足:b≤2a+3c且bc=a2,则
的取值范围是 .
| b |
| a-2c |
考点:利用导数研究函数的单调性,基本不等式
专题:导数的综合应用,不等式的解法及应用
分析:当c>0时满足:b≤2a+3c且bc=a2,可得
≤2a+3c,解得-1≤
≤3.于是
=
=
=f(
),令
=t∈[-1,3],可得f(t)=
,利用导数研究其单调性极值与最值即可得出.
| a2 |
| c |
| a |
| c |
| b |
| a-2c |
| ||
| a-2c |
(
| ||
|
| a |
| c |
| a |
| c |
| t2 |
| t-2 |
解答:
解:当c>0时满足:b≤2a+3c且bc=a2,
∴
≤2a+3c,
化为(
)2-2•
-3≤0,
解得-1≤
≤3.
=
=
=f(
),
令
=t∈[-1,3],
∴f(t)=
=t+2+
,
∴f′(t)=1-
=
.
列出表格:
又f(-1)=-
,f(0)=0,f(3)=9.
由表格可知:f(t)∈(-∞,0]∪[9,+∞).
故答案为:(-∞,0]∪[9,+∞).
∴
| a2 |
| c |

化为(
| a |
| c |
| a |
| c |
解得-1≤
| a |
| c |
| b |
| a-2c |
| ||
| a-2c |
(
| ||
|
| a |
| c |
令
| a |
| c |
∴f(t)=
| t2 |
| t-2 |
| 4 |
| t-2 |
∴f′(t)=1-
| 4 |
| (t-2)2 |
| t(t-4) |
| (t-2)2 |
列出表格:
| t | [-1,0) | 0 | (0,2) | (2,3] |
| f′(t) | + | 0 | - | - |
| f(t) | 单调递增 | 极大值 | 单调递减 | 单调递减 |
| 1 |
| 3 |
由表格可知:f(t)∈(-∞,0]∪[9,+∞).
故答案为:(-∞,0]∪[9,+∞).
点评:本题考查了一元二次不等式的解法、利用导数研究函数的单调性极值与最值,考查了推理能力与计算能力,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在正方体ABCD-A1B1C1D1中,A1D与BC1所成的角为( )
| A、30° | B、45° |
| C、60° | D、90° |
在同一坐标系下函数y=-x+a和y=ax图象可能是( )
A、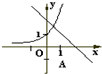 |
B、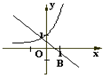 |
C、 |
D、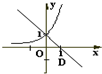 |
设
、
都是非零向量,下列四个条件中,一定能使
+
=
成立的是( )
| a |
| b |
| ||
| |a| |
| ||
| |b| |
| 0 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知两点A(-2,1),B(1,5),点C是圆(x-1)2+(y+2)2=9上的动点,则△ABC面积的最大值为( )
| A、36 | B、18 | C、16 | D、8 |
