题目内容
(本小题满分13分)已知椭圆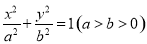 的离心率为
的离心率为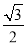 ,且过点
,且过点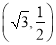 .
.
(I)求椭圆的标准方程;
(II)四边形ABCD的顶点在椭圆上,且对角线AC,BD过原点O,设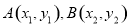 ,满足
,满足 .
.
(i)试证 的值为定值,并求出此定值;
的值为定值,并求出此定值;
(ii)试求四边形ABCD面积的最大值.
(Ⅰ)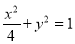 ;(Ⅱ)(i)
;(Ⅱ)(i)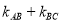 为定值0;(ii)最大值为4.
为定值0;(ii)最大值为4.
【解析】
试题分析:(Ⅰ)利用待定系数法进行求解;(Ⅱ)联立直线与椭圆的方程,整理成关于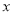 的一元二次方程,利用
的一元二次方程,利用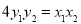 得出定值;利用弦长公式求弦长,即三角形的底边,再利用点到直线的距离公式求其高,进而得出面积,理基本不等式求其最值.
得出定值;利用弦长公式求弦长,即三角形的底边,再利用点到直线的距离公式求其高,进而得出面积,理基本不等式求其最值.
试题解析:(Ⅰ)由题意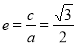 ,
,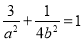 ,又
,又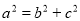 , 2分
, 2分
解得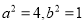 ,
,
椭圆的标准方程为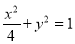 . 4分
. 4分
(Ⅱ) (i) 直线AB的斜率不存在(或AB的斜率为0)时不满足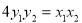
设直线AB的方程为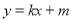 ,设
,设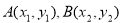
联立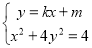 ,得
,得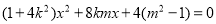
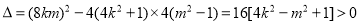 (*)
(*)
 6分
6分
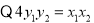
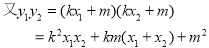 7分
7分
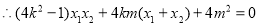
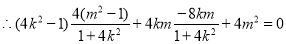 8分
8分
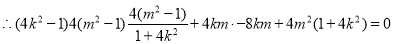
整理得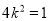
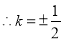
所以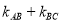 为定值0. 10分
为定值0. 10分
(ii) 由(i),不妨取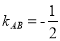 ,则
,则
设原点到直线AB的距离为d,则
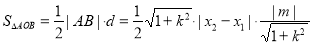 11分
11分
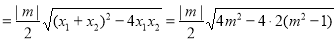
 12分
12分
当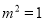 时(满足(*)式)取等号.
时(满足(*)式)取等号.
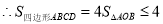 .
.
即四边形ABCD的面积的最大值为4.
考点:1.椭圆的标准方程;2.直线与椭圆的位置关系.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
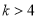 是方程
是方程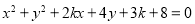 表示圆的充要条件;
表示圆的充要条件;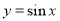 的图象向右平移
的图象向右平移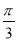 单位,再保持纵坐标不变,横坐标变为原来的
单位,再保持纵坐标不变,横坐标变为原来的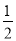 ,得到函数
,得到函数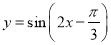 的图象;
的图象;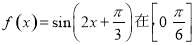 上为增函数;
上为增函数;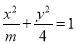 的焦距为2,则实数m的值等于5.
的焦距为2,则实数m的值等于5. 为
为 
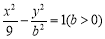 ,过其右焦点
,过其右焦点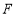 作圆
作圆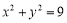 的两条切线,切点记作
的两条切线,切点记作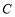 ,
, ,双曲线的右顶点为
,双曲线的右顶点为 ,
,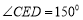 ,则其双曲线的离心率为( )
,则其双曲线的离心率为( )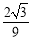 (B)
(B)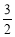 (C)
(C)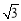 (D)
(D)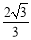
 ,则
,则 的大小关系是( )
的大小关系是( ) (B)
(B) (C)
(C) (D)
(D)
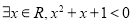 ”的否定是“
”的否定是“ ”;
”; 中,若
中,若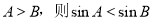 ;
;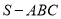 内任取一点P,使得
内任取一点P,使得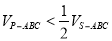 的概率是
的概率是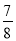 ;
;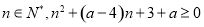 恒成立,则实数a的取值范围是
恒成立,则实数a的取值范围是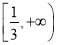 .
.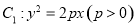 与双曲线
与双曲线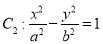
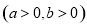 的一条渐近线的交点,若点A到抛物线
的一条渐近线的交点,若点A到抛物线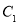 的准线的距离为p,则双曲线
的准线的距离为p,则双曲线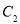 的离心率等于
的离心率等于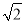 B.
B.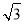 C.
C.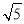 D.
D.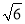
 与曲线
与曲线 恰有一个公共点,则
恰有一个公共点,则 的取值范围是
的取值范围是  则xy的取值范围是 .
则xy的取值范围是 .