题目内容
(12分)已知椭圆的两个焦点为 ,离心率
,离心率 .
.
(1)求椭圆的方程;
(2)设直线 ,若
,若 与椭圆交于
与椭圆交于 两点,且
两点,且 等于椭圆的短轴长,求
等于椭圆的短轴长,求 的值;
的值;
(3)若直线 ,若
,若 与椭圆交于两个不同的点A和B,且使
与椭圆交于两个不同的点A和B,且使 ,问这样的直线存在吗?若存在求
,问这样的直线存在吗?若存在求 的值,若不存在说明理由。
的值,若不存在说明理由。
(1) (2)
(2) (3)
(3)
【解析】
试题分析: (1)由题知:  ,
, ,求出
,求出 ,然后这写出方程(2)直线与椭圆联立,利用韦达定理写出
,然后这写出方程(2)直线与椭圆联立,利用韦达定理写出 ,再利用弦长公式,列出方程
,再利用弦长公式,列出方程 ,解出
,解出 (3)∵
(3)∵ 则
则  同样利用韦达定理列出方程,解出
同样利用韦达定理列出方程,解出
试题解析:(1) ,
, ;
;
联立直线与椭圆 ,得
,得 ,所以
,所以
(2)设
 ,
,
又∵ 此时△ > 0
此时△ > 0
(3)设 
 ∵
∵  则
则 
所以 ,
,
∴
 此时△> 0
此时△> 0
考点:椭圆方程,直线与椭圆方程的应用

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
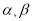 是两个不同的平面,以下说法正确的有 (填所有真命题的序号)
是两个不同的平面,以下说法正确的有 (填所有真命题的序号)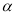 ,则m⊥
,则m⊥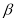 ,
,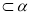 ,则
,则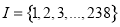 ,若
,若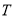 是
是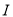 的子集且满足条件:当
的子集且满足条件:当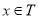 时,
时,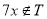 ,则集合
,则集合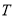 中元素的个数最多是( )
中元素的个数最多是( )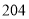 B.
B.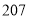 C.
C. D.
D.
 .
. 的图象,只需将函数
的图象,只需将函数 的图象上所有点( )
的图象上所有点( ) 个单位长度,再把横坐标缩短为原来的
个单位长度,再把横坐标缩短为原来的 倍(纵坐标不变)
倍(纵坐标不变) 个单位长度,再把横坐标缩短为原来的
个单位长度,再把横坐标缩短为原来的 被圆
被圆 截得的弦长为__________.
截得的弦长为__________. B.
B. C.
C. D.
D.
 =4,动点P满足
=4,动点P满足 ,则
,则 的最小值为 .
的最小值为 . 有最小值,则a的取值范围是( )
有最小值,则a的取值范围是( )