题目内容
设连续正整数的集合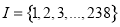 ,若
,若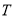 是
是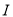 的子集且满足条件:当
的子集且满足条件:当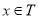 时,
时,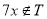 ,则集合
,则集合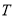 中元素的个数最多是( )
中元素的个数最多是( )
A.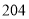 B.
B.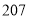 C.
C.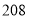 D.
D.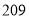
C
【解析】
试题分析:集合T中不能有满足7倍关系的两个数,因此我们将I中的数分成三类:
第一类:1,7,49;2,14,98;3,21,147;4,28,196;共4组,每组最多只能有两个数在集合T中,即集合T中至少需要排除其中4个元素:7,14,21,18;
第二类:5,35;6,42;8,56;…;34,238,;共30-4=26组;每组最多只能有一个数在集合T中,即集合T中至少需要排除其中的26个元素;
第三类:不在上面两类中的所有数:36,37,38,…,237,它们不是7的倍数,且它们的7倍不在集合I中,所以这组中所有数都可以在集合T中;
所以集合T中最多可以有238-4-26=208个元素.
考点:排列组合问题.

练习册系列答案
相关题目
 是实数集R上的奇函数.
是实数集R上的奇函数. 的值;
的值; 是
是 上的单调增函数;
上的单调增函数; 是正方形,
是正方形, ,
, ,且
,且 ,
, ,
, .
.
 与
与 交于点
交于点 ,求证:
,求证:  平面
平面 ;
; 平面
平面 ;
; 的余弦值.
的余弦值.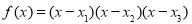 ,
,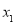 ,
,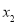 ,
,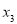
 ,且
,且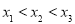 .
.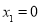 ,
,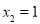 ,
,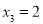 时,若方程
时,若方程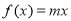 恰存在两个相等的实数根,求实数
恰存在两个相等的实数根,求实数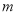 的值;
的值;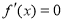 有两个不相等的实数根;
有两个不相等的实数根;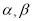
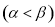 ,试比较
,试比较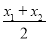 与
与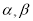 的大小并说明理由.
的大小并说明理由.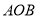 的边
的边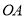 上有异于顶点
上有异于顶点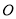 的6个点,边
的6个点,边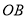 上有异于顶点
上有异于顶点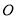 ,以这11个点为顶点共可以组成 个三角形(用数字作答).
,以这11个点为顶点共可以组成 个三角形(用数字作答). 的图象为
的图象为 ,下面结论中正确的是( )
,下面结论中正确的是( ) 的最小正周期是
的最小正周期是
 对称
对称 的图象向右平移
的图象向右平移 个单位得到
个单位得到 上是增函数
上是增函数 .求:
.求: 的对称轴方程;
的对称轴方程; 上的最值。
上的最值。 ,离心率
,离心率 .
. ,若
,若 与椭圆交于
与椭圆交于 两点,且
两点,且 等于椭圆的短轴长,求
等于椭圆的短轴长,求 的值;
的值; ,问这样的直线存在吗?若存在求
,问这样的直线存在吗?若存在求 中,“
中,“ ”是“
”是“ ”的( )
”的( )