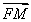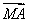题目内容
已知F是双曲线C：
的右焦点，O是双曲线C的中心，直线y=
是双曲线C的一条渐近线．以线段OF为边作正三角形MOF，若点M在双曲线C上，则m的值为 ．
【答案】分析：依题意，m=
，M（
c，
c），将M点的坐标代入双曲线方程可得到关于m的方程，解之即可．
解答：解：∵F（c，0）是双曲线C：
-
=1（a＞0，b＞0）的右焦点，直线y=
是双曲线C的一条渐近线，
又双曲线C的一条渐近线为y=
x，
∴m=
，
又点M在双曲线C上，△MOF为正三角形，
∴M（
c，
c），
∴
-
=1，又c2=a2+b2，
∴
-
=1，
即
+
m-
-
=1，
∴m2-6m-3=0，又m＞0，
∴m=3+2
．
故答案为：3+2
．
点评：本题考查双曲线的简单性质，考查其渐近线方程，考查代入法与解方程的能力，属于难题．
，M（c，c），将M点的坐标代入双曲线方程可得到关于m的方程，解之即可．解答：解：∵F（c，0）是双曲线C：
-=1（a＞0，b＞0）的右焦点，直线y=是双曲线C的一条渐近线，又双曲线C的一条渐近线为y=
x，∴m=
，又点M在双曲线C上，△MOF为正三角形，
∴M（
c，c），∴
-=1，又c2=a2+b2，∴
-=1，即
+m--=1，∴m2-6m-3=0，又m＞0，
∴m=3+2
．故答案为：3+2
．点评：本题考查双曲线的简单性质，考查其渐近线方程，考查代入法与解方程的能力，属于难题．
练习册系列答案
相关题目
