题目内容
已知F是双曲线C:
-
=1 (a>0,b>0)的左焦点,B1B2是双曲线的虚轴,M是OB1的中点,过F,M的直线交双曲线C于点A,且
=2
,则双曲线C的离心率是
.
| x2 |
| a2 |
| y2 |
| b2 |
| FM |
| MA |
| 5 |
| 2 |
| 5 |
| 2 |
分析:设A(x0,y0),由题设知M(0,
),F(-c,0),故
=(c,
),
=(x0,y0-
),由
=2
,解得x0=
,y0=
b,把A(
,
b)代入双曲线C:
-
=1 (a>0,b>0),能够求出双曲线C的离心率.
| b |
| 2 |
| FM |
| b |
| 2 |
| MA |
| b |
| 2 |
| FM |
| MA |
| c |
| 2 |
| 3 |
| 4 |
| c |
| 2 |
| 3 |
| 4 |
| x2 |
| a2 |
| y2 |
| b2 |
解答:解:设A(x0,y0),
由题设知M(0,
),F(-c,0),
∴
=(c,
),
=(x0,y0-
),
∵
=2
,
∴c=2x
,
=2(y0-
),
解得x0=
,y0=
b,
∵A(
,
b)在双曲线C:
-
=1 (a>0,b>0)上,
∴
-
=1,
∴
=
,
∴双曲线C的离心率e=
.
故答案为:
.
由题设知M(0,
| b |
| 2 |
∴
| FM |
| b |
| 2 |
| MA |
| b |
| 2 |
∵
| FM |
| MA |
∴c=2x
0 |
| b |
| 2 |
| b |
| 2 |
解得x0=
| c |
| 2 |
| 3 |
| 4 |
∵A(
| c |
| 2 |
| 3 |
| 4 |
| x2 |
| a2 |
| y2 |
| b2 |
∴
| ||
| a2 |
| ||
| b2 |
∴
| c2 |
| a2 |
| 25 |
| 4 |
∴双曲线C的离心率e=
| 5 |
| 2 |
故答案为:
| 5 |
| 2 |
点评:本题考查双曲线的性质及其应用,解题时要认真审题,仔细解答,注意向量性质的灵活运用.

练习册系列答案
相关题目
 已知双曲线C:
已知双曲线C: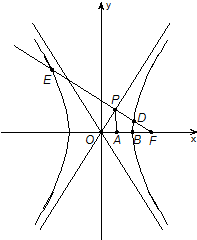 已知双曲线C:
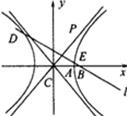
已知双曲线C: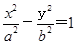 (a>0,b>0)的左焦点,E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A、B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围为(
)
(a>0,b>0)的左焦点,E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A、B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围为(
)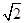 ) D.(2,1+
) D.(2,1+