题目内容
已知F是双曲线C:
-
=1(a>0,b>0)右焦点,若F到双曲线C的渐近线的距离是1,且双曲线C的离心率e=
.
(1)求双曲线C的方程;
(2)过点A(0,1)的直线l与双曲线C的右支交于不同两点P、Q,且P在A、Q之间,若
=
,求直线l的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求双曲线C的方程;
(2)过点A(0,1)的直线l与双曲线C的右支交于不同两点P、Q,且P在A、Q之间,若
| AP |
| 1 |
| 2 |
| AQ |
分析:(1)根据双曲线的右焦点F到渐近线的距离是1,得,
=1,根据双曲线C的离心率e=
得,
=
,再结合双曲线中a,b,c的关系,解出a,b,就求出双曲线C的方程.
(2)设点P(x1,y1),Q(x2,y2),设出直线l的方程,与双曲线方程联立,求出x1+x2,x1x2,根据
=
得到一个关于k的等式,解k,即可求出直线l的方程
| bc | ||
|
| ||
| 2 |
| c |
| a |
| ||
| 2 |
(2)设点P(x1,y1),Q(x2,y2),设出直线l的方程,与双曲线方程联立,求出x1+x2,x1x2,根据
| AP |
| 1 |
| 2 |
| AQ |
得到一个关于k的等式,解k,即可求出直线l的方程
解答:解:(1)由对称性,不妨设一渐近线为y=
x,右焦点为F(c,0),
则
=1,即b=1又e=
=
∴解得a2=2,所以双曲线C的方程是
-y2=1;
(2)设直线l的斜率为k,则l的方程为y=kx+1,设点P(x1,y1),Q(x2,y2),
由
得:(1-2k2)x2-4kx-4=0,
∵l与双曲线C的右支交于不同的两点P、Q,
∴
∴
<k2<1且k<0①
又∵
=
,∴(x1,y1-1)=
(x2,y2-1)x2=2x1
∴3x1=
,3x1=
∴9x1x2=
=9×
,k=±
满足①式.
∴直线l的方程为y=
x+1或y=-
x+1
| b |
| a |
则
| bc | ||
|
| c |
| a |
| ||
| 2 |
∴解得a2=2,所以双曲线C的方程是
| x2 |
| 2 |
(2)设直线l的斜率为k,则l的方程为y=kx+1,设点P(x1,y1),Q(x2,y2),
由
|
∵l与双曲线C的右支交于不同的两点P、Q,
∴
|
∴
| 1 |
| 2 |
又∵
| AP |
| 1 |
| 2 |
| AQ |
| 1 |
| 2 |
∴3x1=
| -4k |
| 2k2-1 |
| -8k |
| 2k2-1 |
∴9x1x2=
| 32k2 |
| (2k2-1)2 |
| 4 |
| 2k2-1 |
3
| ||
| 10 |
∴直线l的方程为y=
3
| ||
| 10 |
3
| ||
| 10 |
点评:本题主要考查了双曲线方程的求法,以及根据直线与双曲线位置求直线方程,属于圆锥曲线的常规题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
 已知双曲线C:
已知双曲线C: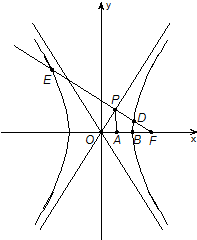 已知双曲线C:
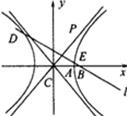
已知双曲线C: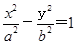 (a>0,b>0)的左焦点,E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A、B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围为(
)
(a>0,b>0)的左焦点,E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A、B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围为(
)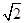 ) D.(2,1+
) D.(2,1+