题目内容
已知{an}满足an+1=
,a1=1.
(1)求数列{an}的通项公式.
(2)设cn=(an+1)an+1,求数列{cn}的前n项和Sn.
| an | an+2 |
(1)求数列{an}的通项公式.
(2)设cn=(an+1)an+1,求数列{cn}的前n项和Sn.
分析:(1)对已知an+1=
等号两端取倒数,易证数列{
+1}是首项为2,公比为2的等比数列,从而可求数列{an}的通项公式;
(2)将(1)中所求的an=
代入cn=(an+1)an+1,列项后整理可得cn=
-
,从而可求数列{cn}的前n项和Sn.
| an |
| an+2 |
| 1 |
| an |
(2)将(1)中所求的an=
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
解答:解:(1)∵
=
=1+
,
∴
+1=2(1+
),即
=2,又
+1=2,
∴数列{
+1}是首项为2,公比为2的等比数列,
∴
+1=2•2n-1=2n,
∴an=
.
(2)∵cn=(an+1)an+1=(
+1)•
=
=
-
,
∴Sn=(
-
)+(
-
)+…+(
-
)
=1-
.
| 1 |
| an+1 |
| an+2 |
| an |
| 2 |
| an |
∴
| 1 |
| an+1 |
| 1 |
| an |
| ||
|
| 1 |
| a1 |
∴数列{
| 1 |
| an |
∴
| 1 |
| an |
∴an=
| 1 |
| 2n-1 |
(2)∵cn=(an+1)an+1=(
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
| 2n |
| (2n-1)(2n+1-1) |
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
∴Sn=(
| 1 |
| 21-1 |
| 1 |
| 22-1 |
| 1 |
| 22-1 |
| 1 |
| 23-1 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
=1-
| 1 |
| 2n+1-1 |
点评:本题考查数列的求和,着重考查等比关系的确定与裂项法求和,对已知“an+1=
”等号两端取倒数是关键,考查观察、分析与运算能力,属于中档题.
| an |
| an+2 |

练习册系列答案
相关题目
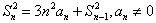 ,n=2,3,4,…
,n=2,3,4,… 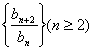 是常数数列;
是常数数列;