题目内容
已知An(an,bn)(n∈N*)是曲线y=ex上的点,a1=a,Sn是数列{an}的前n项和,且满足:
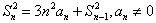 ,n=2,3,4,…
,n=2,3,4,…
(Ⅰ)证明数列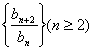 是常数数列;
是常数数列;
(Ⅱ)确定a的取值集合M,使a∈M时,数列{an}是单调递增数列;
(Ⅲ)证明当a∈M时,弦AnAn+1(n∈N*)的斜率随n单调递增。
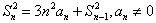 ,n=2,3,4,…
,n=2,3,4,… (Ⅰ)证明数列
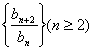 是常数数列;
是常数数列;(Ⅱ)确定a的取值集合M,使a∈M时,数列{an}是单调递增数列;
(Ⅲ)证明当a∈M时,弦AnAn+1(n∈N*)的斜率随n单调递增。
解:(Ⅰ)当n≥2时,由已知得 ,
,
因为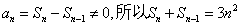 , …………①
, …………①
于是 , …………②
, …………②
由②-①得 , …………③
, …………③
于是 , …………④
, …………④
由④-③得 , …………⑤
, …………⑤
所以 (n≥2)是常数列。
(n≥2)是常数列。
(Ⅱ)由①有 ,
,
由③有 ,
,
而⑤表明:数列 分别是以a2、a3为首项,6为公差的等差数列,
分别是以a2、a3为首项,6为公差的等差数列,
所以 ,
,
数列 是单调递增数列
是单调递增数列 对任意的k∈N*成立
对任意的k∈N*成立

 ,
,
即所求a的取值集合是 。
。
(Ⅲ)弦 ,
,
任取x0,设函数 ,
,
记 ,
,
当 上为增函数,
上为增函数,
当 上为减函数,
上为减函数,
所以 ,从而f′(x)>0,
,从而f′(x)>0,
所以f(x)在 上都是增函数;
上都是增函数;
由(Ⅱ)知,当a∈M时,数列 单调递增,
单调递增,
取 ;
;
取 ;
;
所以 的斜率随n单调递增。
的斜率随n单调递增。
 ,
,因为
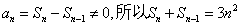 , …………①
, …………① 于是
 , …………②
, …………② 由②-①得
 , …………③
, …………③ 于是
 , …………④
, …………④ 由④-③得
 , …………⑤
, …………⑤ 所以
 (n≥2)是常数列。
(n≥2)是常数列。(Ⅱ)由①有
 ,
,由③有
 ,
,而⑤表明:数列
 分别是以a2、a3为首项,6为公差的等差数列,
分别是以a2、a3为首项,6为公差的等差数列,所以
 ,
,数列
 是单调递增数列
是单调递增数列 对任意的k∈N*成立
对任意的k∈N*成立
 ,
,即所求a的取值集合是
 。
。(Ⅲ)弦
 ,
,任取x0,设函数
 ,
,记
 ,
,当
 上为增函数,
上为增函数,当
 上为减函数,
上为减函数,所以
 ,从而f′(x)>0,
,从而f′(x)>0,所以f(x)在
 上都是增函数;
上都是增函数;由(Ⅱ)知,当a∈M时,数列
 单调递增,
单调递增,取
 ;
;取
 ;
;所以
 的斜率随n单调递增。
的斜率随n单调递增。 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目