题目内容
16．已知正方体ABCD-A1B1C1D1的棱长为1，过正方体ABCD-A1B1C1D1的对角线BD1的截面面积为S，则S的取值范围是[$\frac{\sqrt{6}}{2}，\sqrt{2}$]．分析 由题意画出图形，根据棱AA1上的点到对角线BD1的距离可得使截面面积取得最值的情形，则面积S的取值范围可求．
解答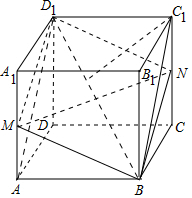 
解：由图可知，当M、N分别为AA1、CC1 的中点时，截面面积最小为$\frac{1}{2}×MN×B{D}_{1}=\frac{1}{2}\sqrt{2}×\sqrt{3}=\frac{\sqrt{6}}{2}$；
当截面为ABC1D1 时，截面面积最大为$1×\sqrt{2}=\sqrt{2}$．
∴S的取值范围是[$\frac{\sqrt{6}}{2}，\sqrt{2}$]．
故答案为：[$\frac{\sqrt{6}}{2}，\sqrt{2}$]．
点评 本题考查棱柱的结构特征，考查数形结合的解题思想方法，属中档题．
练习册系列答案
相关题目
7．已知集合A={x|x2+3x≤0}，集合B={n|n=2k+1，k∈Z}，则A∩B=（ ）
| A． | {-1，1} | B． | {1，3} | C． | {-3，-1} | D． | {-3，-1，1，3} |
11．
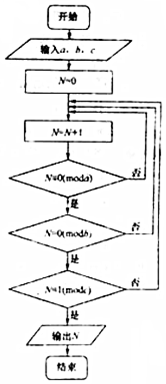若正整数N除以正整m后的余数为n，则记为N=n（modm），例如10=4（mod6）．如图程序框图的算法源于我国古代《孙子算经》中的“孙子定律”的某一环节，执行该框图，输入a=2，b=3，c=5，则输出的N=（ ）
若正整数N除以正整m后的余数为n，则记为N=n（modm），例如10=4（mod6）．如图程序框图的算法源于我国古代《孙子算经》中的“孙子定律”的某一环节，执行该框图，输入a=2，b=3，c=5，则输出的N=（ ）| A． | 6 | B． | 9 | C． | 12 | D． | 21 |
4．已知集合A={3，a2}，B={2，1-a，b}，且A∩B={1}，则A∪B=（ ）
| A． | {0，1，3} | B． | {1，2，3} | C． | {1，2，4} | D． | {0，1，2，3} |