题目内容
直线l的方程为y+kx+1=0，则直线l恒过的定点为 ．
考点：恒过定点的直线
专题：直线与圆
分析：令k的系数为0，即当x=0时，无论k如何取值，y恒为-1，从而可得答案．
解答：
解：∵直线l的方程为y+kx+1=0，
∴当x=0时，无论k如何取值，y恒为-1，即直线l恒过的定点（0，-1），
故答案为：（0，-1）．
∴当x=0时，无论k如何取值，y恒为-1，即直线l恒过的定点（0，-1），
故答案为：（0，-1）．
点评：本题考查恒过定点的直线，k的系数为0是解决问题的关键，属于基础题．
练习册系列答案
相关题目
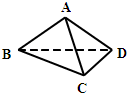如图，四面体A-BCD中，AB=AD=CD=1，BD=| 2 |
A、
| ||||
| B、3π | ||||
C、
| ||||
| D、2π |
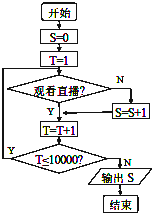为了解“伦敦奥运会开幕式”电视直播节目的收视情况，某机构在某地随机抽查了10000人，把抽查结果输入如图所示的程序框图中，其输出的数值是3700，则该节目的收视率为（ ）| A、3700 | B、630 |
| C、0.63 | D、0.37 |
已知集合A={y|y=-x2+1，x∈R}，B={y|y=2x，x∈R}则（ ）
| A、A⊆B |
| B、B⊆A |
| C、∁RA⊆B |
| D、B⊆∁RA |