题目内容
11.已知f(x)=log4(x+b),点(1,6)关于直线y=x的对称点在函数f(x)的图象上.(1)求b的值;
(2)若f(a+2)+f(a+1)-f(a+8)=1,求实数a的值.
分析 (1)确定对称点(6,1)在函数f(x)的图象上,得出方程log4(6+b)=1,求解即可得出b的值.
(2)化简得出log4a+log4(a-1)-log2(a+6)=1.转化为$\left\{\begin{array}{l}{a>0}\\{a-1>0}\\{a+6>0}\\{\frac{a(a-1)}{a+6}=4}\end{array}\right.$求解即可得出a的值.
解答 解:(1)∵f(x)=log4(x+b),点(1,6)关于直线y=x的对称点在函数f(x)的图象上,
∴(6,1)在函数f(x)的图象上,
即log4(6+b)=1,
得出b=-2.
(2)f(x)=log4(x-2),
∵f(a+2)+f(a+1)-f(a+8)=1,
∴log4a+log4(a-1)-log4(a+6)=1.
即$\left\{\begin{array}{l}{a>0}\\{a-1>0}\\{a+6>0}\\{\frac{a(a-1)}{a+6}=4}\end{array}\right.$即a=8或a=-3(舍去),
故实数a的值为:8.
点评 本题考查了函数的图象的对称性问题,解对数方程的方法,转化思想的运用,属于中档题.

练习册系列答案
相关题目
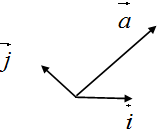 如图,在同一平面内,向量$\overrightarrow a$与单位向量$\overrightarrow i、\overrightarrow j$的夹角分别为30°、90°,已知$|\overrightarrow a|$=$2\sqrt{3}$
如图,在同一平面内,向量$\overrightarrow a$与单位向量$\overrightarrow i、\overrightarrow j$的夹角分别为30°、90°,已知$|\overrightarrow a|$=$2\sqrt{3}$