题目内容
已知函数f(x)=
满足对任意x1≠x2,都有
<0成立,则a的取值范围是 .
|
| f(x1)-f(x2) |
| x1-x2 |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:根据已知条件可知函数f(x)在R上单调递减,所以对于ax,0<a<1;对于(a-3)x+4a,a<3,又ax>1,所以(a-3)x+4a的最大值满足小于等于1,而(a-3)x+4a对于x≥0时的最大值为4a,所以4a≤1,所以得到a≤
,和前面的0<a<1的a的取值求交集即得a的取值范围.
| 1 |
| 4 |
解答:
解:∵对任意x1≠x2,都有
<0成立;
∴f(x1)-f(x2)与x1-x2异号,
即x1-x2<0时,f(x1)-f(x2)>0,即x1<x2时,f(x1)>f(x2);
∴函数f(x)在R上是减函数;
∴x<0时,f(x)=ax,0<a<1;
x≥0时,f(x)=(a-3)x+4a,a-3<0,a<3,又ax>1,((a-3)x+4a)max=4a≤1,
∴a≤
;
又0<a<1,∴0<a≤
;
∴a的取值范围是(0,
].
故答案为:(0,
].
| f(x1)-f(x2) |
| x1-x2 |
∴f(x1)-f(x2)与x1-x2异号,
即x1-x2<0时,f(x1)-f(x2)>0,即x1<x2时,f(x1)>f(x2);
∴函数f(x)在R上是减函数;
∴x<0时,f(x)=ax,0<a<1;
x≥0时,f(x)=(a-3)x+4a,a-3<0,a<3,又ax>1,((a-3)x+4a)max=4a≤1,
∴a≤
| 1 |
| 4 |
又0<a<1,∴0<a≤
| 1 |
| 4 |
∴a的取值范围是(0,
| 1 |
| 4 |
故答案为:(0,
| 1 |
| 4 |
点评:考查单调性的定义,分段函数的单调性,指数函数的单调性,一次函数的单调性,以及对于单调性定义的利用.

练习册系列答案
相关题目
 在平面向量中有如下定理:设点O、P、Q、R为同一平面内的点,则P、Q、R三点共线的充要条件是:存在实数t,使
在平面向量中有如下定理:设点O、P、Q、R为同一平面内的点,则P、Q、R三点共线的充要条件是:存在实数t,使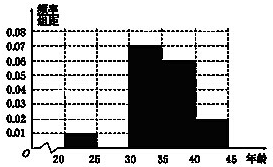 对某项活动中800名青年志愿者的年龄抽样调查后,得到如图所示的频率分布直方图,但年龄在25,30)的数据不慎丢失.依据此图,估计该项活动中年龄在25,30)的志愿者人数为
对某项活动中800名青年志愿者的年龄抽样调查后,得到如图所示的频率分布直方图,但年龄在25,30)的数据不慎丢失.依据此图,估计该项活动中年龄在25,30)的志愿者人数为
 函数f(x)=2sin(ωx+φ)(ω>0,
函数f(x)=2sin(ωx+φ)(ω>0,