题目内容
已知直线l1:x+my-1=0,l2:mx+(m+2)y+1=0;(Ⅰ)若l1∥l2,求m的值;
(Ⅱ)若l1⊥l2,求m的值.
【答案】分析:(I)根据两条直线平行的条件,可得两个方程的一次项系数对应成比例,且不等于常数项的比.由此建立关于m的方程,解之即可得到实数m的值.
(II)由两条直线垂直的条件,建立关于m的方程,解之可得实数m的值.
解答:解:(I)∵l1∥l2,
∴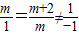 ,解之得m=2(舍去-1)、
,解之得m=2(舍去-1)、
即m的值为2;
(II)∵l1⊥l2,
∴1×m+m×(m+2)=0,解之得m=0或-3
即m的值为0或-3.
点评:本题给出含有参数的两条直线方程,在两条直线平行或垂直的情况下,求参数m之值.着重考查了平面直角坐标系中两条直线平行、垂直的关系及其列式的知识,属于基础题.
(II)由两条直线垂直的条件,建立关于m的方程,解之可得实数m的值.
解答:解:(I)∵l1∥l2,
∴
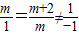 ,解之得m=2(舍去-1)、
,解之得m=2(舍去-1)、即m的值为2;
(II)∵l1⊥l2,
∴1×m+m×(m+2)=0,解之得m=0或-3
即m的值为0或-3.
点评:本题给出含有参数的两条直线方程,在两条直线平行或垂直的情况下,求参数m之值.着重考查了平面直角坐标系中两条直线平行、垂直的关系及其列式的知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目