题目内容

14．已知x，y满足$\left\{\begin{array}{l}x≥2\\ x+y≤4\\ 2x-y-m≤0\end{array}\right.$，若目标函数z=3x+y的最大值为10，则m的值为5．

分析 作出不等式组对应的平面区域，根据z的几何意义，利用数形结合即可得到m的值．然后即可得到结论．

解答 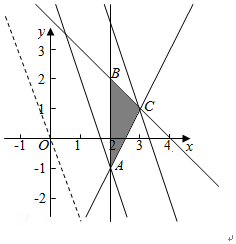解：不等式组对应的平面区域如图：
由z=3x+y得y=-3x+z
平移直线y=-3x+z，则由图象可知当直线y=-3x+z经过点C时，直线y=-3x+z的截距最大，此时z最大，为3x+y=10
由$\left\{\begin{array}{l}{3x+y=10}\\{x+y=4}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$，即C（3，1），
此时C在2x-y-m=0上，
则m=5．
故答案为：5．

点评 本题主要考查线性规划的应用，根据z的几何意义，利用数形结合是解决本题的关键．

练习册系列答案
相关题目
4．{an}是首项为1，公差为3的等差数列，如果an=2 014，则序号n等于（　　）
A．667B．668C．669D．672
5．设a，b是两条不同的直线，α，β为两个不重合的平面，下列命题中的真命题的是（　　）
A．若a，b与α所成的角相等，则a∥bB．若a∥α，b∥β，α∥β，则a∥b
C．若a?α，b?β，α⊥β，则 a⊥bD．若a⊥α，b⊥β，α∥β，则a∥b
2．求下列函数的导数：
（1）$y=2{x^3}+\root{3}{x}+cosx-1$
（2）y=（x3+1）（2x2+8x-5）
（3）$y=\frac{{lnx+{2^x}}}{x^2}$．
9．平面直角坐标系xoy中，椭圆C1：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{{\sqrt{2}}}{2}$，过椭圆右焦点F作两条相互垂直的弦，当其中一条弦所在直线斜率为0时，两弦长之和为6．
（1）求椭圆的方程；
（2）A，B是抛物线C2：x2=4y上两点，且A，B处的切线相互垂直，直线AB与椭圆C1相交于C，D两点，求弦|CD|的最大值．
19．如图，在矩形ABCD中，$AB=\sqrt{3}，BC=1$，将△ACD沿折起，使得D折起的位置为D1，且D1在平面ABC的射影恰好落在AB上，在四面体D1ABC的四个面中，其中有n对平面相互垂直，则n等于（　　）
A．2B．3C．4D．5
6．已知函数f（x）的导数f'（x），f（x）不是常数函数，且（x+1）f（x）+xf'（x）≥0，对x∈[0，+∞）恒成立，则下列不等式一定成立的是（　　）
A．ef（1）＜f（2）B．f（1）＜0C．ef（e）＜2f（2）D．f（1）＜2ef（2）
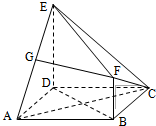2．在多面体ABCDEF中，四边形ABCD为正方形，AD=DE=2BF=2，ED⊥平面ABCD，FB∥ED．
（1）若$\overrightarrow{FG}=\frac{1}{2}（\overrightarrow{FA}+\overrightarrow{FE}）$，求证：FG∥平面ABCD；
（2）求二面角B-EF-C的大小．
3．已知a，b，c为三条不重合的直线，α，β，γ为三个不重合的平面，给出四个命题：
①$\left.\begin{array}{l}{α∥c}\\{β∥c}\end{array}\right\}$⇒α∥β；②$\left.\begin{array}{l}{α∥γ}\\{β∥γ}\end{array}\right\}$⇒α∥β；③$\left.\begin{array}{l}{α∥c}\\{a∥c}\end{array}\right\}$⇒a∥α；④$\left.\begin{array}{l}{a∥γ}\\{β∥γ}\end{array}\right\}$⇒a∥β
其中正确的命题是（　　）
A．①②③B．①④C．②D．①③④

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网