题目内容

直线x=
π
3
的倾斜角等于（　　）
A、0
B、
π
3
C、
π
2
D、不存在
考点：直线的倾斜角
专题：直线与圆
分析：利用直线性质求解．
解答： 解：∵直线x=
π
3
垂直于x轴，
∴直线x=
π
3
的倾斜角为
π
2
．
故选：C．
点评：本题考查直线的倾斜角的求法，是基础题，解题时要认真审题，注意直线性质的灵活运用．
练习册系列答案
相关题目
已知直线y=kx+1 与抛物线x2=4y 相交于A，B两点，且该抛物线过A，B两点的切线交于C，点C的轨迹记为E，M，N是E上不同的两点，直线AM，BN都与y轴平行，则
FM
•
FN
=
 
．
若z=cosθ+isinθ（i为虚数单位），则使z2=-1的θ的取值为
 
．
数列{an}满足an=
2n-1，1≤n≤10
219-n，11≤n≤19
，则该数列从第5项到第15项的和为（　　）
A、2016B、1528
C、1504D、992
函数f（x）=x2sinx（x∈R）是（　　）
A、奇函数B、偶函数
C、增函数D、减函数
在△ABC中，角A，B，C的对边分别是a，b，c．已知a=5
2
，c=10，A=30°，则B等于（　　）
A、105°
B、60°
C、15°
D、105° 或 15°
设l，m是不同的直线，α，β是不同的平面．若l⊥α，m⊥β，有下面四个命题：
（1）α∥β⇒l∥m；
（2）α⊥β⇒l⊥m；
（3）l∥m⇒α⊥β；
（4）l⊥m⇒α∥β
其中正确的命题是（　　）
A、（1）（2）
B、（2）（4）
C、（1）（3）
D、（3）（4）
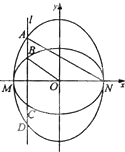如图，已知椭圆C1的中心在原点O，长轴左、右端点M，N在x轴上，椭圆C2的短轴为MN，且C1，C2的离心率都为e，直线l⊥MN，l与C1交于两点，与C2交于两点，这四点按纵坐标从大到小依次为A，B，C，D，且BO∥AN，则离心率e的范围是（　　）
A、
2
2
＜e＜1
B、0＜e＜
2
2
C、0＜e＜
1
2
D、
1
2
＜e＜1
复数z=
1
1+i
（i为虚数单位），则z的共轭复数
.
z
是（　　）
A、
1
2
-
1
2
i
B、
1
2
+
1
2
i
C、-
1
2
-
1
2
i
D、-
1
2
+
1
2
i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网