题目内容
在△ABC中,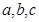 分别为角A、B、C的对边,
分别为角A、B、C的对边,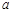 =3,△ABC的面积为6,
=3,△ABC的面积为6, ,D为△ABC内任一点,点D到三边距离之和为
,D为△ABC内任一点,点D到三边距离之和为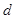 。
。
(1)求:角A的正弦值;
(2)求:边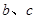 ;
;
(3)求: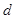 的取值范围
的取值范围
(1) ;⑵b=4,c=5或b=5,c=4.⑶
;⑵b=4,c=5或b=5,c=4.⑶
解析试题分析:(1)根据正弦定理把 转化为
转化为 ,即可求得
,即可求得 ,得到
,得到 .⑵根据三角形的面积公式可得
.⑵根据三角形的面积公式可得 ,又
,又 ,
,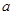 =3,可解得b=4,c=5或b="5,c=" 4 .⑶设D到三边的距离分别为x、y、z,则
=3,可解得b=4,c=5或b="5,c=" 4 .⑶设D到三边的距离分别为x、y、z,则 ,
, ,消去z可得
,消去z可得 ,画出不等式表示的平面区域可求得d的范围.
,画出不等式表示的平面区域可求得d的范围.
试题解析: (1) 





 4分
4分
(2)
 ,
, 20,由
20,由 及
及 20与
20与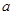 =3解得b=4,c=5或b="5,c=4" . 8分
=3解得b=4,c=5或b="5,c=4" . 8分
(3)设D到三边的距离分别为x、y、z,则 ,
, ,
,
又x、y满足 ,画出不等式表示的平面区域得:
,画出不等式表示的平面区域得: . 12分
. 12分
考点:1.正弦定理;2.三角形的面积3.线性规划的最优解.

练习册系列答案
相关题目
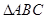 中,角
中,角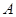 ,
,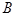 ,
,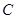 对应的边分别是
对应的边分别是 ,
,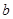 ,
,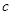 .已知
.已知 .
. ,
,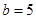 ,求
,求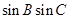 的值.
的值.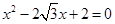 的两个根,且
的两个根,且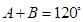 ,求△ABC的面积及AB的长.
,求△ABC的面积及AB的长.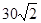 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西 方向的
方向的 处,此时两船相距
处,此时两船相距 海里,当甲船航行
海里,当甲船航行 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西 方向的
方向的 处,此时两船相距
处,此时两船相距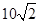 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
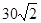 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于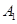 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西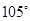 方向的
方向的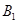 处,此时两船相距
处,此时两船相距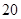 海里,当甲船航行
海里,当甲船航行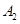 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西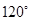 方向的
方向的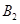 处,此时两船相距
处,此时两船相距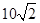 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?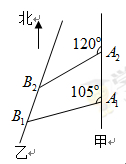
 、
、 是方程
是方程 的两根,角
的两根,角 、
、 满足
满足 ,求角
,求角 的度数,边
的度数,边 的长度及
的长度及 的面积.
的面积.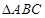 中,a,b,c分别为内角A,B,C的对边,已知:
中,a,b,c分别为内角A,B,C的对边,已知: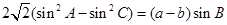 ,
,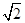 .
.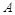 、
、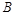 、
、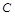 的对边分别为
的对边分别为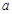 、
、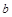 、
、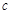 ,设S为△ABC的面积,满足
,设S为△ABC的面积,满足 .
.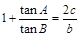 ,且
,且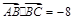 ,求
,求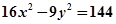 ,
,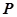 在双曲线上,满足
在双曲线上,满足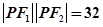 ,求
,求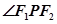 的大小.
的大小.