题目内容
已知双曲线的方程是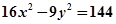 ,
,
(1)求此双曲线的焦点坐标、离心率和渐近线方程;
(2)点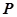 在双曲线上,满足
在双曲线上,满足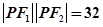 ,求
,求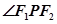 的大小.
的大小.
(1) ,
, ,
, ;(2)
;(2)
解析试题分析:(1)将双曲线方程化为标准方程 ,所以
,所以 ,焦点
,焦点 ,离心率为
,离心率为 ,渐近线方程为
,渐近线方程为 ;(2)在
;(2)在 中,
中, =10,又知道另外两边
=10,又知道另外两边 、
、 的关系:
的关系: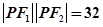 ,求
,求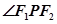 ,可想到余弦定理,利用余弦定理
,可想到余弦定理,利用余弦定理 ,又想到双曲线的定义
,又想到双曲线的定义 ,所以继续变形为
,所以继续变形为 =0,所以
=0,所以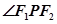 =
= .
.
试题解析:(1)双曲线方程化为标准方程 ,所以
,所以 ,∴焦点为
,∴焦点为 ,离心率为
,离心率为 ,渐近线方程为
,渐近线方程为 ;
;
(2)因为点 在双曲线上,所以
在双曲线上,所以 ,在
,在 中,
中, =
= =0,∴
=0,∴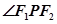 =
= .
.
考点:1、双曲线的简单几何性质;2、双曲线的定义;3、余弦定理.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
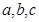 分别为角A、B、C的对边,
分别为角A、B、C的对边,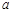 =3,△ABC的面积为6,
=3,△ABC的面积为6, ,D为△ABC内任一点,点D到三边距离之和为
,D为△ABC内任一点,点D到三边距离之和为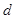 。
。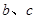 ;
; 中,
中, ,
,  的大小;
的大小; 时,求
时,求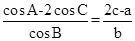 .
.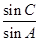 的值;
的值; ,
,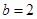 ,求
,求 的面积.
的面积.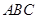 中,内角
中,内角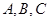 所对的边分别为
所对的边分别为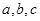 ,已知m
,已知m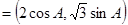 ,n
,n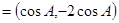 ,m·n
,m·n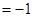 .
. 的大小;
的大小;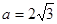 ,
, ,求△
,求△ ,
,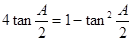 .
.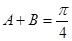 ;
;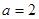 ,求c和ΔABC的面积.
,求c和ΔABC的面积.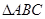 中,角
中,角 的对边分别为
的对边分别为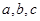 ,
, ,
,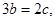
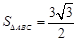 .
.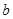 的值;
的值;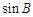 的值.
的值. 中,
中, 分别为角
分别为角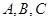 所对的三边,
所对的三边,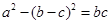 ,
,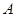 ;
;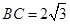 ,角
,角 等于
等于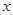 ,周长为
,周长为 ,求函数
,求函数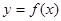 的取值范围.
的取值范围.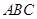 中,
中,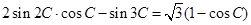 .
.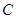 的大小;
的大小; ,且
,且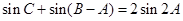 ,求
,求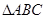 的面积.
的面积.