题目内容
20.直角三角形ABC中,AB=3,AC=4,BC=5,点M是三角形ABC外接圆上任意一点,则$\overrightarrow{AB}•\overrightarrow{AM}$的最大值为12.分析 建立坐标系,设M ($\frac{3}{2}+\frac{5}{2}cosα,2+\frac{5}{2}sinα$),则 $\overrightarrow{AM}$=($\frac{3}{2}+\frac{5}{2}cosα,2+\frac{5}{2}sinα$),$\overrightarrow{AB}=(3,0)$,$\overrightarrow{AB}•\overrightarrow{AM}=\frac{9}{2}+\frac{15}{2}cosα≤12$
解答 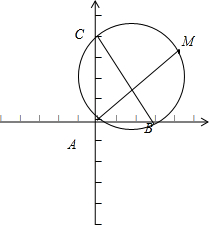 解:如图建立平面直角坐标系,A(0,0),B(3,0),C(0.4),
解:如图建立平面直角坐标系,A(0,0),B(3,0),C(0.4),
三角形ABC外接圆(x-$\frac{3}{2}$)2+(y-2)2=$\frac{25}{4}$,
设M ($\frac{3}{2}+\frac{5}{2}cosα,2+\frac{5}{2}sinα$),则 $\overrightarrow{AM}$=($\frac{3}{2}+\frac{5}{2}cosα,2+\frac{5}{2}sinα$),$\overrightarrow{AB}=(3,0)$,
$\overrightarrow{AB}•\overrightarrow{AM}=\frac{9}{2}+\frac{15}{2}cosα≤12$,
故答案为:12.
点评 本题考查了圆的参数方程、三角函数的单调性、数量积坐标运算,考查了推理能力与计算能力,属于中档题

练习册系列答案
相关题目
10.从装有2个红球和 2个白球的口袋内任取2个,则互斥但不对立的两个事件是( )
| A. | 至少一个白球与都是白球 | B. | 至少一个白球与至少一个红球 | ||
| C. | 恰有一个白球与 恰有2个白球 | D. | 至少一个白球与都是红球 |
5.已知y=g(x)与y=h(x)都是定义在(-∞,0)∪(0,+∞)上的奇函数,且当x>0时,$g(x)=\left\{\begin{array}{l}{x^2},\;\;0<x≤1\\ g(x-1),\;\;\;x>1.\end{array}\right.$,h(x)=klog2x(x>0),若y=g(x)-h(x)恰有4个零点,则正实数k的取值范围是( )
| A. | $[\frac{1}{2},1]$ | B. | $(\frac{1}{2},1]$ | C. | $(\frac{1}{2},{log_3}2]$ | D. | $[\frac{1}{2},{log_3}2]$ |
