题目内容

将一圆形纸片沿半径剪开为两个扇形，其圆心角之比为3：4，再将它们卷成两个圆锥侧面，则两圆锥的高之比为
 
．
考点：旋转体（圆柱、圆锥、圆台）,棱锥的结构特征
专题：综合题,空间位置关系与距离
分析：设出圆形纸片的半径，根据两个扇形圆心角之比，得到扇形的弧长之比，得到两个圆锥的底面半径之比，得到两个圆锥的高之比．
解答： 解：设圆形纸片的半径是r，
∴沿半径剪开为两个扇形，其圆心角之比为3：4时，两个扇形的弧长分别是
8πr
7
，
6πr
7
，
围成圆锥时两个圆锥的底面半径分别是
4r
7
，
3r
7
，
两个圆锥的母线长度相等，都是r，
∴两个圆锥的高分别是
2
10
r
7
，
33
r
7

∴两圆锥的高之比为2
10
：
33
，
故答案为：2
10
：
33
．
点评：本题考查旋转体中的圆锥，考查圆锥用扇形围成的过程中各个量之间的关系，本题是一个运算量比较大的题目，是一个中档题．
练习册系列答案
相关题目
复数
3-3i
1-i
（i是虚数单位）的实部和虚部的和是（　　）
A、4B、6C、2D、3
平面上两点F1，F2满足|F1F2|=10．设d为实数，令Γ表示平面上满足||PF1|-|PF2||=d的所有P点所成的图形．又令圆C为平面上以F1为圆心，9为半径的圆．给出下列选项：
①当d=0时，Γ为直线；
②当d=1时，Γ为双曲线；
③当d=6时，Γ9与C有两个公共点；
④当d=8时，Γ与C有三个公共点；
⑤当d=10时，Γ与C有两个公共点．
其中是真命题的有：
 
．（把你认为正确命题的序号都填上）
关于曲线C：
|x|
5
+
|y|
4
=1，下列四个命题中，所有真命题的组合是（　　）
①曲线C上的横、纵坐标的取值范围分别是-5≤x≤5，-4≤y≤4；
②曲线C关于x轴、y轴都是对称的，还关于原点对称；
③设P，Q是曲线C上的任意两点，则|PQ|≤10恒成立；
④设M（-3，0），N（3，0），P是曲线C上任意的点，则|PM|+|PN|≤10恒成立．
A、①②③④B、①②③
C、①②④D、①②
下列命题中：
①函数f（x）=lg（x2+mx+m）的值域为R，则m∈（0，4）；
②若函数f（x）满足f（x+1）=
1+f(x)
1-f(x)
，则f（x）为周期函数；
③函数y=f（2-x）与y=f（2+x）的图象关于直线x=2对称；
④若函数f(x)=x+log2(x+
x2+1
)，则“m+n≥0”是“f（m）+f（n）≥0”的充要条件．
其中正确命题的序号是
 
．
已知椭圆方程为
x2
4b2
+
y2
b2
=1，直线y=-x-1与椭圆交于A，B，且OA⊥OB，求椭圆方程．
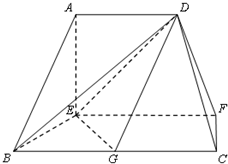在如图的多面体中，EF⊥平面AEB，AE⊥EB，AD∥EF∥BC，BC=2AD=4，AE=BE=2，G是BC的中点．
（1）求证：AB∥平面DEG；
（2）求直线BD与平面BCFE所成角的正切值；
（3）求证：BD⊥EG．
已知向量
OA
=3i-4j，
OB
=6i-3j，
OC
=（5-m）i-（3+m）j，其中i，j分别是平面直角坐标系内x轴与y轴正方向上的单位向量．
（1）若点A，B，C能构成三角形，求实数m应满足的条件；
（2）对任意m∈[1，2]，不等式
AC
2≤-x2+x+3恒成立，求x的取值范围．
三棱锥P-ABC中，M、N、K分别是△PAB，△PBC，△PAC的重心，S△ABC=18．
（1）求证：MN
∥
.
1
3
AC；
（2）求S△MNK．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网