题目内容
已知函数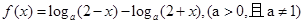
(1)判断函数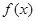 的奇偶性,并说明理由。
的奇偶性,并说明理由。
(2)若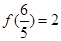 ,求使
,求使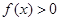 成立
成立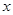 的集合。
的集合。
(1) 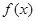 是奇函数;(2)
是奇函数;(2) 
解析试题分析:(1)首先求出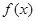 的定义域关于原点对称,然后求
的定义域关于原点对称,然后求 与
与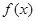 关系,利用对数的运算法则将函数转化为
关系,利用对数的运算法则将函数转化为 ,再由函数奇偶性的定义
,再由函数奇偶性的定义 判断
判断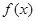 是奇函数;
是奇函数;
(2)由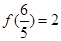 求出
求出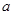 ,利用函数的定义域和单调性求出不等式的解集;易忘记定义域.
,利用函数的定义域和单调性求出不等式的解集;易忘记定义域.
试题解析:
(1)由 的定义域为
的定义域为
且
所以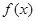 是奇函数
是奇函数
(2) 

 即
即




 解得
解得
所以使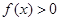 成立
成立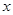 的集合
的集合 .
.
考点:对数函数性质,复合函数奇偶性.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度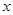 (单位:
(单位: )满足关系:
)满足关系:
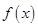 为隔热层建造费用与20年的能源消耗费用之和。
为隔热层建造费用与20年的能源消耗费用之和。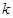 的值及
的值及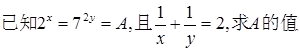
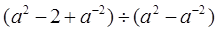
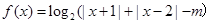 .
. 时,求函数
时,求函数 的定义域;
的定义域; 的不等式
的不等式 的解集是
的解集是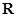 ,求
,求 的取值范围.
的取值范围.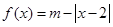 ,
,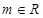 ,且
,且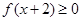 的解集为
的解集为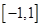 .
.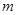 的值;
的值;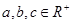 ,且
,且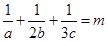 ,求证:
,求证: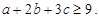
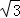 海里的速度前往拦截.
海里的速度前往拦截.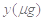 与服药后的时间
与服药后的时间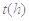 之间近似满足如图所示的曲线.其中
之间近似满足如图所示的曲线.其中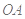 是线段,曲线段
是线段,曲线段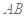 是函数
是函数
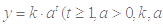 是常数
是常数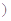 的图象.
的图象.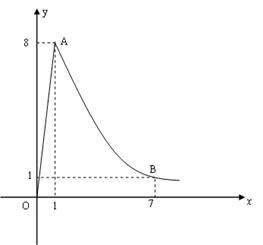
 关于时间
关于时间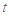 的函数关系式;
的函数关系式;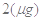 时治疗有效,假若某病人第一次服药为早上
时治疗有效,假若某病人第一次服药为早上 ,为保持疗效,第二次服药最迟是当天几点钟?
,为保持疗效,第二次服药最迟是当天几点钟?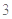
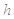 ,该病人每毫升血液中含药量为多少
,该病人每毫升血液中含药量为多少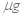 ?
?
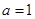 时,求函数
时,求函数 在
在 的值域;
的值域;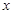 的方程
的方程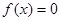 有解,求
有解,求 的取值范围.
的取值范围.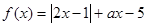 (a是常数,a∈R)
(a是常数,a∈R)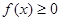 的解集;
的解集;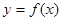 恰有两个不同的零点,求a的取值范围.
恰有两个不同的零点,求a的取值范围.