题目内容
已知函数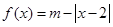 ,
,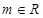 ,且
,且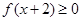 的解集为
的解集为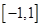 .
.
(Ⅰ)求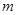 的值;
的值;
(Ⅱ)若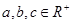 ,且
,且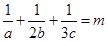 ,求证:
,求证: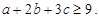
(Ⅰ) ;(Ⅱ)见解析.
;(Ⅱ)见解析.
解析试题分析:(Ⅰ)将问题转化为 有解,且其解集为
有解,且其解集为 ,又
,又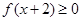 解集为
解集为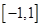 ,所以
,所以 ;(Ⅱ)利用柯西不等式解答.
;(Ⅱ)利用柯西不等式解答.
试题解析:(1)因为 ,
,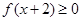 等价于
等价于 , 2分
, 2分
由 有解,得
有解,得 ,且其解集为
,且其解集为 ,又
,又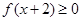 解集为
解集为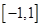 ,所以
,所以 . 5分
. 5分
(2)由(1)知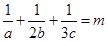 ,又
,又 ,由柯西不等式得
,由柯西不等式得 10分
10分
考点:柯西不等式的应用、函数和不等式.

练习册系列答案
相关题目
题目内容
已知函数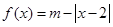 ,
,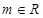 ,且
,且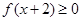 的解集为
的解集为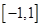 .
.
(Ⅰ)求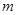 的值;
的值;
(Ⅱ)若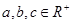 ,且
,且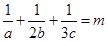 ,求证:
,求证: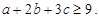
(Ⅰ) ;(Ⅱ)见解析.
;(Ⅱ)见解析.
解析试题分析:(Ⅰ)将问题转化为 有解,且其解集为
有解,且其解集为 ,又
,又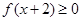 解集为
解集为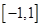 ,所以
,所以 ;(Ⅱ)利用柯西不等式解答.
;(Ⅱ)利用柯西不等式解答.
试题解析:(1)因为 ,
,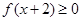 等价于
等价于 , 2分
, 2分
由 有解,得
有解,得 ,且其解集为
,且其解集为 ,又
,又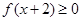 解集为
解集为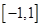 ,所以
,所以 . 5分
. 5分
(2)由(1)知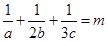 ,又
,又 ,由柯西不等式得
,由柯西不等式得 10分
10分
考点:柯西不等式的应用、函数和不等式.
