题目内容
某医药研究所开发一种新药,据监测,如果成人按规定剂量服用该药,服药后每毫升血液中的含药量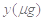 与服药后的时间
与服药后的时间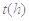 之间近似满足如图所示的曲线.其中
之间近似满足如图所示的曲线.其中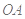 是线段,曲线段
是线段,曲线段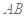 是函数
是函数
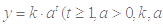 是常数
是常数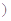 的图象.
的图象.
(1)写出服药后每毫升血液中含药量 关于时间
关于时间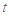 的函数关系式;
的函数关系式;
(2)据测定:每毫升血液中含药量不少于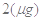 时治疗有效,假若某病人第一次服药为早上
时治疗有效,假若某病人第一次服药为早上 ,为保持疗效,第二次服药最迟是当天几点钟?
,为保持疗效,第二次服药最迟是当天几点钟?
(3)若按(2)中的最迟时间服用第二次药,则第二次服药后再过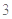
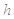 ,该病人每毫升血液中含药量为多少
,该病人每毫升血液中含药量为多少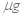 ?
?
(1) ;(2)上午
;(2)上午 ;(3)
;(3) .
.
解析试题分析:(1)注意观察图形,区分清楚每一段图形所表示的函数表达式;(2)显然第二次服药时间应该在第二段曲线上,有 ;(3)第二次服药后3
;(3)第二次服药后3 ,血液中含药量包含第一次服药的剩余量和第二次服药的剩余量.
,血液中含药量包含第一次服药的剩余量和第二次服药的剩余量.
试题解析:(1)当 时,
时, ; 2分
; 2分
当 时,把
时,把 代如
代如 ,得
,得 ,解得
,解得 ,
,
故 . 5分
. 5分
(2)设第一次服药最迟过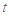 小时服第二次药,则
小时服第二次药,则 解得
解得 ,即第一次服药后
,即第一次服药后 后服第二次药,也即上午
后服第二次药,也即上午 服药; 9分
服药; 9分
(3)第二次服药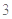
 后,每毫升血液中含第一次服药后的剩余药量为:
后,每毫升血液中含第一次服药后的剩余药量为:
含第二次所服的药量为: .所以
.所以 .
.
故该病人每毫升血液中的喊药量为 . 13分
. 13分
考点:函数的图象与函数的应用.

练习册系列答案
相关题目
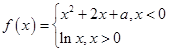 ,其中
,其中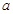 是实数,设
是实数,设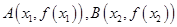 为该函数的图象上的两点,且
为该函数的图象上的两点,且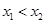 .
. 的单调区间;
的单调区间;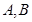 处的切线互相垂直,且
处的切线互相垂直,且 ,求
,求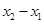 的最小值;
的最小值;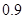 万元,年维修费用第一年是
万元,年维修费用第一年是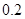 万元,第二年是
万元,第二年是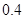 万元,第三年是
万元,第三年是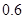 万元,…,以后逐年递增
万元,…,以后逐年递增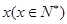 年的维修费用的和为
年的维修费用的和为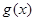 ,年平均费用为
,年平均费用为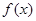 .
.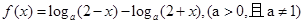
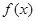 的奇偶性,并说明理由。
的奇偶性,并说明理由。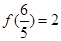 ,求使
,求使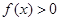 成立
成立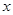 的集合。
的集合。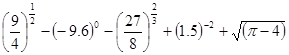 ;
;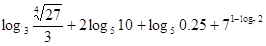 .
.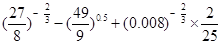 ;
;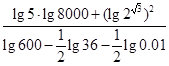 .
.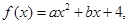 集合
集合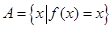
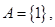 求函数
求函数 的解析式;
的解析式;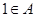 ,且
,且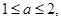 设
设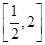 上的最大值、最小值分别为
上的最大值、最小值分别为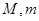 ,记
,记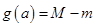 ,求
,求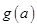 的最小值.
的最小值.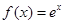 ,
,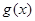 为其反函数.
为其反函数. 与
与 与
与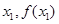 )、(
)、(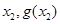 ),且
),且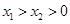 ,求证:
,求证: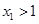 .
.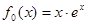 ,
,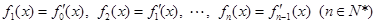 .
.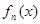 的表达式(不需证明);
的表达式(不需证明);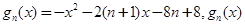 的最大值为
的最大值为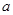 ,
,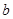 ,求
,求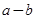 的最小值.
的最小值.