题目内容
已知二次函数f(x)=ax2+bx+c(a≠0)经过A(-1,0),B(5,0),C(0,-
)三点.
(1)求f(x)的解析式;
(2)求f(2),画出函数f(x)的图象,并根据其图象出该函数的定义域与值域.
| 5 |
| 2 |
(1)求f(x)的解析式;
(2)求f(2),画出函数f(x)的图象,并根据其图象出该函数的定义域与值域.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)把A(-1,0),B(5,0),C(0,-
)三点的坐标代入函数的解析式,列方程组求得a、b、c的值,可得函数的解析式.
(2)由函数的解析式求得f(2)的值,再利用二次函数的性质求得二次函数的定义域和值域.
| 5 |
| 2 |
(2)由函数的解析式求得f(2)的值,再利用二次函数的性质求得二次函数的定义域和值域.
解答:
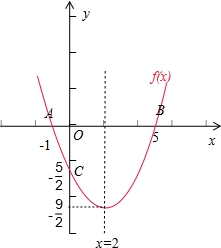 解:(1)根据f(x)=ax2+bx+c(a≠0)经过A(-1,0),
解:(1)根据f(x)=ax2+bx+c(a≠0)经过A(-1,0),
B(5,0),C(0,-
)三点,
可得
,由此求得
,f(x)=
x2-2x-
.
(2)由以上可得f(2)=2-4-
=-
,
显然二次函数的定义域为R,由它的最小值为
=-
,
可得函数的值域为[-
,+∞).
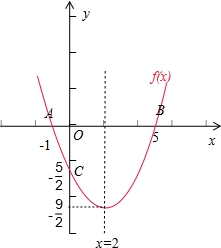 解:(1)根据f(x)=ax2+bx+c(a≠0)经过A(-1,0),
解:(1)根据f(x)=ax2+bx+c(a≠0)经过A(-1,0),B(5,0),C(0,-
| 5 |
| 2 |
可得
|
|
| 1 |
| 2 |
| 5 |
| 2 |
(2)由以上可得f(2)=2-4-
| 5 |
| 2 |
| 9 |
| 4 |
显然二次函数的定义域为R,由它的最小值为
4×
| ||||
| 2 |
| 9 |
| 2 |
可得函数的值域为[-
| 9 |
| 2 |
点评:本题主要考查用待定系数法求函数的解析式,二次函数的性质应用,属于基础题.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.