题目内容
【题目】为了研究某种微生物的生长规律,研究小组在实验室对该种微生物进行培育实验.前三天观测的该微生物的群落单位数量分别为12,16,24.根据实验数据,用y表示第![]() 天的群落单位数量,某研究员提出了两种函数模型;①
天的群落单位数量,某研究员提出了两种函数模型;①![]() ;②
;②![]() ,其中a,b,c,p,q,r都是常数.
,其中a,b,c,p,q,r都是常数.
(1)根据实验数据,分别求出这两种函数模型的解析式;
(2)若第4天和第5天观测的群落单位数量分别为40和72,请从这两个函数模型中选出更合适的一个,并计算从第几天开始该微生物群落的单位数量超过1000.
【答案】(1)函数模型:①![]() ;函数模型②:
;函数模型②:![]() (2)函数模型②更合适;从第9天开始该微生物群落的单位数量超过1000
(2)函数模型②更合适;从第9天开始该微生物群落的单位数量超过1000
【解析】
(1)由题意利用待定系数法求函数的解析式;
(2)将![]() ,
,![]() 代入(1)中的两个函数解析式中,结合数据判断两个模型中那个更合适。
代入(1)中的两个函数解析式中,结合数据判断两个模型中那个更合适。
(1)由题意,对于函数模型①:把![]() 代入
代入![]() 得
得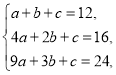
解得![]() ,
,![]() ,
,![]() ,所以
,所以![]() .
.
对于函数模型②:把![]() 代入
代入![]() 得
得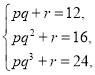
解得![]() ,
,![]() ,
,![]() ,所以
,所以![]() .
.
(2)将![]() ,
,![]() 代入函数模型①,得
代入函数模型①,得![]() ,
,![]() ,不符合观测数据;
,不符合观测数据;
将![]() ,
,![]() 代入函数模型②,得
代入函数模型②,得![]() ,
,![]() ,符合观测数据.
,符合观测数据.
所以函数模型②更合适.
令![]() ,因为
,因为![]() ,可得
,可得![]() ,
,
即从第9天开始该微生物群落的单位数量超过1000.

练习册系列答案
相关题目



