题目内容
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,过
,过![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() .当
.当![]() 轴时,
轴时,![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)由已知条件得b2=a2﹣1,利用通径公式得出|AB|的表达式,再由△ABM的面积得出有关a的方程,求出a的值,可得出椭圆C的标准方程;
(2)对直线l与x轴垂直、与y轴垂直以及与斜率存在且不为零三种情况讨论.在前两种情况下可直接进行验证;在第三种情况下,设直线l的方程为y=k(x﹣1)(k≠0),将直线l的方程与椭圆方程联立,列出韦达定理,利用斜率公式并代入韦达定理,通过化简计算得出结论成立.
(1)依题意得![]() ,即
,即![]() ,
,
所以当![]() 时,解得
时,解得![]() ,当
,当![]() 轴时,
轴时,![]() ,
,
因为![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)当![]() 与
与![]() 轴重合时,
轴重合时,![]() ,满足条件;当
,满足条件;当![]() 与
与![]() 轴垂直时,满足条件,
轴垂直时,满足条件,
当![]() 与
与![]() 轴不重合且不垂直时,设
轴不重合且不垂直时,设![]() 为
为![]() ,
,![]() ,
,![]() ,
,
把![]() 代入
代入![]() ,得
,得![]() ,
,
则![]() ,
,![]() ,
,
因为![]()
![]() ,
,
而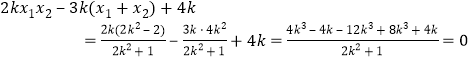 ,
,
所以![]() .
.

练习册系列答案
相关题目


