题目内容
18.若函数f(x)=log2(-x2+ax)的图象过点(1,2),则函数f(x)的值域为(-∞,log2$\frac{25}{4}$].分析 把(1,2)代入f(x)求出a,得到f(x)的解析式,判断真数的取值范围,根据对数函数的单调性得出f(x)的最值,得到值域.
解答 解:f(1)=log2(-1+a)=2,解得a=5.∴f(x)=log2(-x2+5x).由f(x)有意义得-x2+5x>0,
又∵-x2+5x=-(x-$\frac{5}{2}$)2+$\frac{25}{4}$≤$\frac{25}{4}$,∴0<-x2+5x≤$\frac{25}{4}$.
∴f(x)≤log2$\frac{25}{4}$,
故答案为(-∞,log2$\frac{25}{4}$].
点评 本题考查了对数函数的性质,二次不等式的解法,属于中档题.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
8.已知F是抛物线x2=4y的焦点,直线y=kx-1与该抛物线交于第一象限内的两点A,B,若|AF|=4|FB|,则k的值是( )
| A. | $\frac{5}{4}$ | B. | $\frac{3}{4}\sqrt{2}$ | C. | $\frac{{\sqrt{17}}}{4}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
6.若复数$\frac{a-3i}{1+i}$(a∈R,i为虚数单位)是纯虚数,则实数a的值为( )
| A. | 3 | B. | -3 | C. | 0 | D. | $\frac{3}{2}$ |
10.已知直线l与抛物线y2=4x相切于点M,与其准线相交于点N,以MN为直径的圆过x轴上一个定点P,则定点P的坐标为( )
| A. | (-1,0) | B. | (1,0) | C. | (2,0) | D. | (4,0) |
7.函数$f(x)=\sqrt{1-x}+{2^x}$的定义域为( )
| A. | (0,1) | B. | (0,1] | C. | (-∞,1] | D. | [1,+∞) |
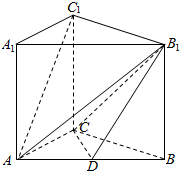 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.