题目内容
19．下列函数是偶函数的是（ ）| A． | $y=\frac{1}{x}+x$ | B． | y=x3 | C． | $y=\sqrt{x}$ | D． | y=x2+1 |
分析 根据函数奇偶性的定义进行判断即可．
解答 解：A.$y=\frac{1}{x}+x$的定义域为{x|x≠0}，则f（-x）=-$\frac{1}{x}$-x=-（$\frac{1}{x}$+x）=-f（x），则函数为奇函数，
B．f（-x）=-x3=-f（x），则函数为奇函数．、
C．函数的定义域为[0，+∞），函数为非奇非偶函数．
D．f（-x）=（-x）2+1=x2+1=f（x），则函数为偶函数，
故选：D．
点评 本题主要考查函数奇偶性的判断，比较基础．
练习册系列答案
相关题目
10．已知直线l与抛物线y2=4x相切于点M，与其准线相交于点N，以MN为直径的圆过x轴上一个定点P，则定点P的坐标为（ ）
| A． | （-1，0） | B． | （1，0） | C． | （2，0） | D． | （4，0） |
7．函数$f（x）=\sqrt{1-x}+{2^x}$的定义域为（ ）
| A． | （0，1） | B． | （0，1] | C． | （-∞，1] | D． | [1，+∞） |
4．某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：
（1）根据上面的数据判断，y=ax+b与y=$\frac{c}{x}$+d哪一个适宜作为产品销量y关于单价x的回归方程类型？（给出判断即可，不必说明理由）
（2）根据（1）的判断结果及表中数据，建立y关于x的回归方程；（计算结果保留两位小数）
参考公式其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$．
| 单价x（元） | 0.25 | 0.5 | 1 | 2 | 4 |
| 销量y（件） | 16 | 12 | 5 | 2 | 1 |
（2）根据（1）的判断结果及表中数据，建立y关于x的回归方程；（计算结果保留两位小数）
参考公式其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$．
11．
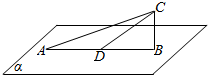如图，平面α⊥平面ABC，D为线段AB的中点，|AB|=2$\sqrt{3}$，∠CDB=30°，P为面α内的动点，且P到直线CD的距离为1，则∠APB的最大值为 ）
如图，平面α⊥平面ABC，D为线段AB的中点，|AB|=2$\sqrt{3}$，∠CDB=30°，P为面α内的动点，且P到直线CD的距离为1，则∠APB的最大值为 ）| A． | 60° | B． | 90° | C． | 120° | D． | 150° |