题目内容
如图,在三棱锥 中,
中, ,
, 平面
平面 ,
, ,
, 分别为
分别为 ,
, 的中点.
的中点.
(1)求证: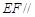 平面
平面 ;
;
(2)求证:平面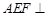 平面
平面 .
.
(1)见解析;(2)见解析
解析试题分析:(1)由E、F分别为PB、PC中点根据三角形中位线定理知EF∥BC,根据线面平行的判定知EF∥面ABC;(2)由PA⊥面PABC知,PA⊥BC,结合AB⊥BC,由线面垂直的判定定理知,BC⊥面PAB,由(1)知EF∥BC,根据线面垂直性质有EF⊥面PAB,再由面面垂直判定定理即可证明面AEF⊥面PAB.
试题解析:证明:(1)在 中,
中, 分别为
分别为 的中点
的中点 3分
3分
又 平面
平面 ,
, 平面
平面
 平面
平面 7分
7分
(2)由条件, 平面
平面 ,
, 平面
平面

 ,即
,即 , 10分
, 10分
由 ,
,
 ,
,
又 ,
, 都在平面
都在平面 内
内 
 平面
平面
又 平面
平面
 平面
平面
 平面
平面 14分
14分
考点:线面垂直的判定与性质;面面垂直判定定理;线面平行判定;推理论证能力

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 中,过对角线
中,过对角线 的一个平面交
的一个平面交 于E,交
于E,交 于F,则
于F,则 一定是平行四边形
一定是平行四边形

 中,底面
中,底面 为直角梯形,且
为直角梯形,且 ,
, ,侧面
,侧面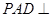 底面
底面 .
. 平面
平面 ;
; 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,指出点
?若存在,指出点 的余弦值.
的余弦值.
 的直径AB=3,点C为
的直径AB=3,点C为 平面ABC,且VC=2,点M为线段VB的中点.
平面ABC,且VC=2,点M为线段VB的中点. 平面VAC;
平面VAC;
 中,
中, ⊥底面
⊥底面 ,底面
,底面 ,
, ,
, 分别是
分别是 ,
, 的 中点.
的 中点. 平面
平面 ;
; ;
; 是线段
是线段 上一动点,试确定
上一动点,试确定 平面
平面 ,并证明你的结论.
,并证明你的结论.

 -A BC中,AB
-A BC中,AB  AC,AB=AC=2,
AC,AB=AC=2, =4,点D是BC的中点.
=4,点D是BC的中点. 与
与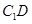 所成角的余弦值;
所成角的余弦值; 与
与 所成二面角的正弦值.
所成二面角的正弦值.
 中,
中, .
.  在对角线
在对角线 上移动,求证:
上移动,求证: ⊥
⊥ ;
; 中点时,求点
中点时,求点 的距离。
的距离。 