题目内容
如图,已知 的直径AB=3,点C为
的直径AB=3,点C为 上异于A,B的一点,
上异于A,B的一点, 平面ABC,且VC=2,点M为线段VB的中点.
平面ABC,且VC=2,点M为线段VB的中点.
(1)求证: 平面VAC;
平面VAC;
(2)若AC=1,求二面角M-VA-C的余弦值.
(1)见解析;(2)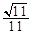
解析试题分析:(1)证明直线与平面垂直的关键是证明该直线与平面内两条相交直线都垂直;(2)求二面角可以利用几何法,先找出二面角的平面角,也可以利用空间坐标系,找出平面的法向量求解.
试题解析:(1)∵ 平面
平面 ,
,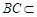 平面
平面
∴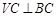 2分
2分
∵点C为 上一点,且AB为直径
上一点,且AB为直径
∴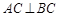 4分
4分
又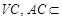 平面VAC,
平面VAC,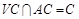
∴ 平面VAC; 6分
平面VAC; 6分
(2)由(1)得,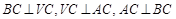
分别以CA,CB,CV所在直线为x轴、y轴、z轴建立空间直角坐标系C-xyz如图所示. 7分
则A(1,0,0),V(0,0,2),B(0,2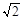 ,0)
,0)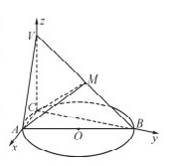
设平面VAC的法向量为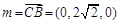 8分
8分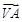 =(1,,,,-2),
=(1,,,,-2),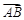 =(-1,2
=(-1,2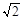 ,0)
,0)
设平面VAM的法向量为n=(x,y,z)
由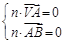 ,得
,得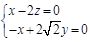
取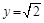 ,得x=4,z=2
,得x=4,z=2
即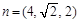 9分
9分
∴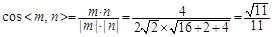 11分
11分
∴二面角M-VA-C的余弦值为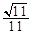 . 12分
. 12分
考点:空间直线与平面垂直的判定,二面角的计算,空间直角坐标系,空间向量的应用.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
 的底面是直角三角形,
的底面是直角三角形, ,点
,点 在底面内的射影恰好是
在底面内的射影恰好是 的中点,且
的中点,且


 平面
平面 ;
; ,求点
,求点 到平面
到平面 的距离.
的距离.
 中,
中, ,
, 平面
平面 ,
, ,
, 分别为
分别为 ,
, 的中点.
的中点. 平面
平面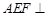 平面
平面 .
.
 .
. 时,求三棱锥F-DEG的体积V.
时,求三棱锥F-DEG的体积V.
 中,底面
中,底面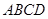 是平行四边形,
是平行四边形, ,
, 平面
平面 ,
, ,
, 是
是 的中点.
的中点. 平面
平面 ;
; 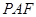 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
 中,
中, .
. 为平行四边形,
为平行四边形, ,
,  ,
,  分别是
分别是 与
与 的中点.
的中点.
 ;
; 的平面角的余弦值.
的平面角的余弦值. 、
、 、
、 是平面,给出下列命题:
是平面,给出下列命题:
 、
、 、
、 是直线,
是直线,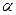 是平面,给出下列命题:①若
是平面,给出下列命题:①若 ,
, ,则
,则 ;
; ,
, ;③若
;③若 ,
, ,则
,则 ,
,