题目内容
如图,在直三棱柱中 -A BC中,AB
-A BC中,AB  AC,AB=AC=2,
AC,AB=AC=2, =4,点D是BC的中点.
=4,点D是BC的中点.
(1)求异面直线 与
与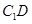 所成角的余弦值;
所成角的余弦值;
(2)求平面 与
与 所成二面角的正弦值.
所成二面角的正弦值.
解析试题分析:(1)以 为单位正交基底建立空间直角坐标系
为单位正交基底建立空间直角坐标系 ,利用向量法能求出异面直线
,利用向量法能求出异面直线 与
与 所成角的余弦值;(2)分别求出平面
所成角的余弦值;(2)分别求出平面 的法向量与
的法向量与 的法向量,利用法向量能求出平面
的法向量,利用法向量能求出平面 与
与 所成二面角的余弦值,再由三角函数知识能求出平面
所成二面角的余弦值,再由三角函数知识能求出平面 与
与 所成二面角的正弦值.
所成二面角的正弦值.
试题解析:(1)以 为单位正交基底建立空间直角坐标系
为单位正交基底建立空间直角坐标系 ,
,
则 ,
, ,
, ,
, ,
, ,
, .
. ,
,

 异面直线
异面直线 与
与 所成角的余弦值为
所成角的余弦值为 .
.
(2) 是平面
是平面 的的一个法向量,设平面
的的一个法向量,设平面 的法向量为
的法向量为 ,
, ,
, ,
,
由 ,
, 得
得 ,取
,取 ,得
,得 ,
, ,
,
所以平面 的法向量为
的法向量为 .
.
设平面 与
与 所成二面角为
所成二面角为 .
. , 得
, 得 .
.
所以平面 与
与 所成二面角的正弦值为
所成二面角的正弦值为 .
.
考点:与二面角有关的立体几何综合题;异面直线及其所成的角.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 中,
中, ,
, 平面
平面 ,
, ,
, 分别为
分别为 ,
, 的中点.
的中点.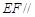 平面
平面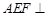 平面
平面 .
.
 中,
中, ,
, ,
, ,
, ,点
,点 是
是 的中点.
的中点.
 ;
; 
 的体积.
的体积. 中,底面
中,底面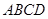 是平行四边形,
是平行四边形, ,
, 平面
平面 ,
, ,
, 是
是 的中点.
的中点. 平面
平面 ;
;  与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
 及其侧视图、俯视图如图所示.设
及其侧视图、俯视图如图所示.设 ,
, 分别为线段
分别为线段 ,
, 的中点,
的中点, 为线段
为线段 上的点,且
上的点,且 .
.
 的余弦值.
的余弦值. 的底面
的底面 是平行四边形,
是平行四边形, ,
, ,
, 分别是棱
分别是棱 的中点.
的中点. 平面
平面 ;
; ,
,
 中,
中, ⊥底面
⊥底面 ,底面
,底面 为侧棱
为侧棱 上一点.
上一点. ,求证:
,求证: 平面
平面 ;
;  ,求证:平面
,求证:平面 .
.
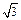 的正三棱锥
的正三棱锥 的外接球的球心为O,满足
的外接球的球心为O,满足 , 则该三棱锥外接球的体积为 .高☆考♂资♀源?网
, 则该三棱锥外接球的体积为 .高☆考♂资♀源?网