题目内容

函数y=sinx与y=x的交点个数为
 
．
考点：正弦函数的图象
专题：三角函数的图像与性质
分析：作出函数y=sinx与y=x的图象，利用数形结合进行求解．
解答： 解：作出函数y=sinx与y=x的图象如图：
则两个图象只有1个交点，
故答案为：1．
点评：本题主要考查函数交点个数的判断，利用数形结合是解决本题的关键．
练习册系列答案
相关题目
由直线2x+y-4=0上任意一点向圆（x+1）2+（y-1）2=1引切线，则切线长的最小值为
 
．
下列五个命题中：
①函数y=loga（2x-1）+2015（a＞0且a≠1）的图象过定点（1，2015）；
②若定义域为R函数f（x）满足：对任意互不相等的x1、x2都有（x1-x2）[f（x1）-f（x2）]＞0，则f（x）是减函数；
③f（x+1）=x2-1，则f（x）=x2-2x；
④若函数f（x）=
a•2x+a-2
2x+1
是奇函数，则实数a=-1；
⑤若a=
logc8
logc2
（c＞0，c≠1），则实数a=3．
其中正确的命题是
 
．（填上相应的序号）．
将函数f（x）=sinx图象上每个点的横坐标变为原来的
1
2
倍（纵坐标不变），再奖得到的图象向右平移
π
12
个单位长度，记所得图象的函数解析式为y=g（x），则g（
π
4
）的值是
 
．
为了得到函数y=sin（2x+
π
6
）的图象，只需把函数y=sin2x图象上所有的点（　　）
A、向左平移
π
3
个单位长度
B、向右平移
π
3
个单位长度
C、向左平移
π
12
个单位长度
D、向右平移
π
12
个单位长度
已知定义在R上的奇函数f（x）满足f（x+2）=-f（x），且当x∈[0，1]时，r（x）=2x-1，则f（7）的值是
 
．
函数y=sin（ωx+φ）的部分图象如图，则φ、ω可以取的一组值是（　　）
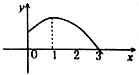
A、ω=
π
2
，φ=
π
4
B、ω=
π
4
，φ=
π
4
C、ω=
π
3
，φ=
π
6
D、ω=
π
4
，φ=
5π
4
若loga
3
4
≥1，则a的取值范围是
 
．
已知直线l：x-2y-1=0，直线l1过点（-1，2）．
（1）若l1⊥l，求直线l1与l的交点坐标；
（2）若l1∥l，求直线l1的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网