题目内容
(本小题满分13分)已知函数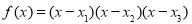 ,
,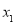 ,
,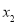 ,
,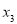
 ,且
,且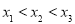 .
.
(Ⅰ)当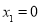 ,
,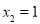 ,
,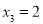 时,若方程
时,若方程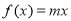 恰存在两个相等的实数根,求实数
恰存在两个相等的实数根,求实数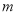 的值;
的值;
(Ⅱ)求证:方程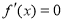 有两个不相等的实数根;
有两个不相等的实数根;
(Ⅲ)若方程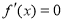 的两个实数根是
的两个实数根是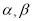
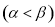 ,试比较
,试比较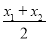 与
与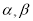 的大小并说明理由.
的大小并说明理由.
(1)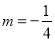 或
或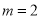 ;(2)证明详见解析;(3)
;(2)证明详见解析;(3)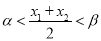 .
.
【解析】
试题分析:本题主要考查方程的根的问题等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,先将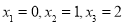 代入到
代入到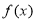 中,将方程
中,将方程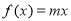 转化为
转化为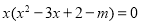 ,有2种情况:第一种:
,有2种情况:第一种: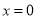 是一元二次方程
是一元二次方程 的一个实数根,第二种:一元二次方程
的一个实数根,第二种:一元二次方程 有两个相等的实数根,分别讨论求解;第二问,展开
有两个相等的实数根,分别讨论求解;第二问,展开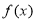 表达式,对
表达式,对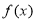 求导,而方程
求导,而方程 的
的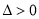 恒成立,所以可证得方程
恒成立,所以可证得方程 有两个不相等的实数根;第三问,将
有两个不相等的实数根;第三问,将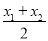 代入
代入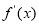 中,可计算得
中,可计算得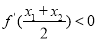 ,而
,而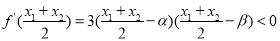 ,解不等式即得
,解不等式即得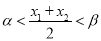 .
.
试题解析:(1)当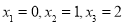 时,
时,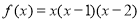 .
.
当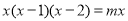 时,
时,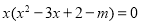 .
.
依题意,若方程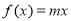 恰存在两个相等的实数根,包括两种情况:
恰存在两个相等的实数根,包括两种情况:
(ⅰ)若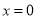 是一元二次方程
是一元二次方程 的一个实数根,则
的一个实数根,则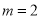 时,方程
时,方程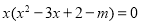 可化为
可化为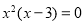 ,恰存在两个相等的实数根0(令一根为3).
,恰存在两个相等的实数根0(令一根为3).
(ⅱ)若一元二次方程 有两个相等的实数根,则方程
有两个相等的实数根,则方程 的根的判别式
的根的判别式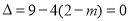 ,解得
,解得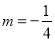 ,此时方程
,此时方程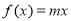 恰存在两个相等的实数根
恰存在两个相等的实数根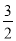 (另一根为0).
(另一根为0).
∴当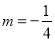 或
或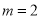 时,方程
时,方程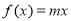 恰存在两个相等的实数根.
恰存在两个相等的实数根.
(2)由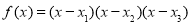 ,可得,
,可得,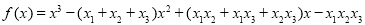 ,
,
∴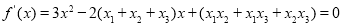 .
.
此一元二次方程的判别式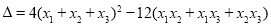 ,
,
则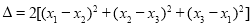 .
.
由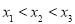 ,可得,
,可得,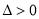 恒成立,
恒成立,
∴方程 有两个不等的实数根.
有两个不等的实数根.
(3)∵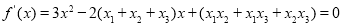 ,
,
得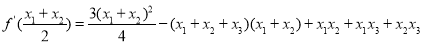
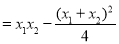
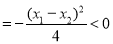
即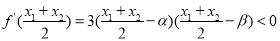 ,由
,由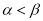 ,得
,得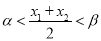 .
.
考点:方程的根的问题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 满足约束条件
满足约束条件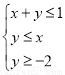 ,则
,则 的最大值为 ( )
的最大值为 ( )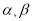 是两个不同的平面,以下说法正确的有 (填所有真命题的序号)
是两个不同的平面,以下说法正确的有 (填所有真命题的序号)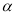 ,则m⊥
,则m⊥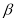 ,
,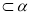 ,则
,则 :
: ,在圆周上随机取一点P,则P到直线
,在圆周上随机取一点P,则P到直线 的距离大于
的距离大于 的概率为 .
的概率为 .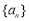 ,则“
,则“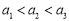 ”是“
”是“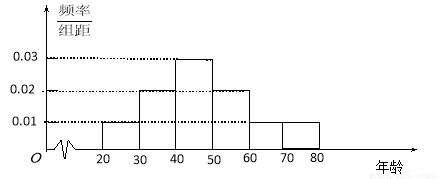
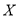 ,求随机变量
,求随机变量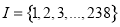 ,若
,若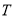 是
是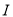 的子集且满足条件:当
的子集且满足条件:当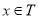 时,
时,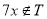 ,则集合
,则集合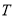 中元素的个数最多是( )
中元素的个数最多是( )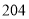 B.
B.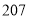 C.
C.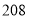 D.
D.
 .
. =4,动点P满足
=4,动点P满足 ,则
,则 的最小值为 .
的最小值为 .