题目内容
(本小题满分13分)退休年龄延迟是平均预期寿命延长和人口老龄化背景下的一种趋势.某机构为了解某城市市民的年龄构成,从该城市市民中随机抽取年龄段在20~80岁(含20岁和80岁)之间的600人进行调查,并按年龄层次[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]绘制频率分布直方图,如图所示.若规定年龄分布在[20,40)岁的人为“青年人”,[40,60)为“中年人”, [60,80]为“老年人”.
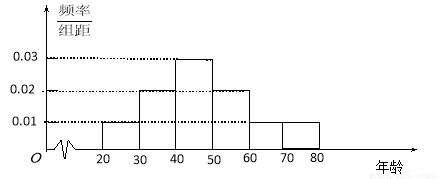
(Ⅰ)若每一组数据的平均值用该区间中点值来代替,试估算所调查的600人的平均年龄;
(Ⅱ)将上述人口分布的频率视为该城市在20-80年龄段的人口分布的概率.从该城市20-80年龄段市民中随机抽取3人,记抽到“老年人”的人数为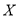 ,求随机变量
,求随机变量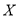 的分布列和数学期望.
的分布列和数学期望.
(1)48岁;(2)分布列详见解析, .
.
【解析】
试题分析:本题主要考查平均值、频率分布直方图、二项分布、随机变量的分布列和数学期望等基础知识,考查学生的分析问题解决问题的能力、计算能力.第一问,用该区间中点值来代替每一组数据的平均值,再乘以每一组数据的频率,得到600人的平均年龄;第二问,先由频率分布直方图确定“老年人”所占的频率为 ,再利用二项分布的概率计算公式,计算出每一种情况的概率,列出分布列,最后利用
,再利用二项分布的概率计算公式,计算出每一种情况的概率,列出分布列,最后利用 计算数学期望.
计算数学期望.
试题解析:(1)由题意估算,所调查的600人的平均年龄为
 .
.
(2)由频率分布直方图可知,“老年人”所占的频率为 .
.
∴从该城市20~80年龄段市民中随机抽取1人,抽到“老年人”的概率为 .
.
依题意,X的可能取值为0,1,2,3.
 ;
;
 ;
;
 ;
;
 .
.
∴随机变量X的分布列如下表:

∴随机变量X的数学期望
 .
.
考点:1.平均值;2.频率分布直方图;3.二项分布;4.随机变量的分布列和数学期望.

 的三个内角
的三个内角 的对边分别是
的对边分别是 ,且
,且 , 则角
, 则角 等于( )
等于( ) B
B  或
或 C
C  D
D 
 在区间[1,3]上的平均变化率为
在区间[1,3]上的平均变化率为  表示的平面区域为D,若函数
表示的平面区域为D,若函数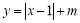 的图像上存在区域D上的点,则实数
的图像上存在区域D上的点,则实数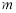 的取值范围是
的取值范围是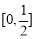 (B)
(B)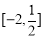
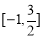 (D)
(D)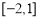
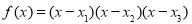 ,
,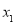 ,
,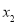 ,
,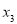
 ,且
,且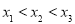 .
.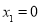 ,
,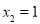 ,
,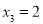 时,若方程
时,若方程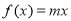 恰存在两个相等的实数根,求实数
恰存在两个相等的实数根,求实数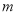 的值;
的值;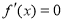 有两个不相等的实数根;
有两个不相等的实数根;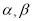
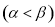 ,试比较
,试比较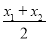 与
与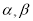 的大小并说明理由.
的大小并说明理由. (
( )的离心率是 ;渐近线方程是 .
)的离心率是 ;渐近线方程是 . 的图象为
的图象为 ,下面结论中正确的是( )
,下面结论中正确的是( ) 的最小正周期是
的最小正周期是
 对称
对称 的图象向右平移
的图象向右平移 个单位得到
个单位得到 上是增函数
上是增函数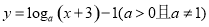 的图象恒过定点A,若点A也在函数
的图象恒过定点A,若点A也在函数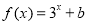 的图象上,则
的图象上,则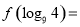 ( )
( ) 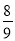 B.
B.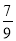 C.
C.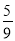 D.
D.
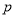 :实数m满足
:实数m满足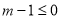 ,命题
,命题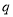 :函数
:函数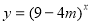 是增函数。若
是增函数。若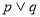 为真命题,
为真命题,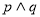 为假命题,则实数m的取值范围为( )
为假命题,则实数m的取值范围为( )