题目内容
18.已知a,b是实数,1和-1是函数f(x)=x3+ax2+bx的两个极值点.(1)求a和b的值;
(2)设函数g(x)的导函数g'(x)=f(x)+2,求g(x)的极值点;
(3)若$h(x)=-\frac{1}{3}(cbx-\frac{bc}{x})+2lnx(c∈R)$,当x1,x2∈(0,+∞)时,不等式$[\frac{{h({x_1})}}{x_2}-\frac{{h({x_2})}}{x_1}]({x_1}-{x_2})<0$恒成立,求c的取值范围.
分析 (1)求出函数f(x)的导数,得到关于a,b的方程组,求出a,b的值;
(2)求出f(x)的解析式,求出g′(x),解关于g′(x)的不等式,求出函数g(x)的单调区间,从而求出g(x)的极值点即可;
(3)求出h(x),整理得x1h(x1)<x2h(x2),根据函数的单调性得到2cx+2+2lnx≤0在(0,+∞)上恒成立,即不等式等价于c≤-$\frac{1+lnx}{x}$(x>0),根据函数的单调性求出c的范围即可.
解答 解:(1)由f(x)=x3+ax2+bx,得f′(x)=3x2+2ax+b,
1和-1是函数f(x)的两个极值点,
∴$\left\{\begin{array}{l}{f′(1)=3+2a+b=0}\\{f′(-1)=3-2a+b=0}\end{array}\right.$,解得a=0,b=-3.
(2)∵由(1)得f(x)=x3-3x,
∴g′(x)=f(x)+2=(x-1)2(x+2),
令g′(x)=0,解得x=1或-2,
∵当x<-2时,g′(x)<0;当-2<x<1时,g′(x)>0,
∴x=-2是g(x)的极值点.
∵当-2<x<1或x>1时,g′(x)>0,
∴x=1不是g(x)的极值点.
∴g(x)的极值点是-2.
(3)由(1)知a=0,b=-3,则h(x)=-$\frac{1}{3}$(cbx-$\frac{bc}{x}$)+2lnx=cx-$\frac{c}{x}$+2lnx,
不妨设x1>x2>0,
所以x1-x2>0,故不等式[$\frac{h{(x}_{1})}{{x}_{2}}$-$\frac{h{(x}_{2})}{{x}_{1}}$](x1-x2)<0,
即$\frac{h{(x}_{1})}{{x}_{2}}$-$\frac{h{(x}_{2})}{{x}_{1}}$<0恒成立,整理得x1h(x1)<x2h(x2),
所以函数y=xh(x)在(0,+∞)上单调递减,
设ω(x)=xh(x),则ω(x)=cx2-c+2xlnx,ω′(x)=2cx+2+2lnx,
由题意得ω′(x)≤0在(0,+∞)上恒成立,
即2cx+2+2lnx≤0在(0,+∞)上恒成立,
因为x>0,所以不等式等价于c≤-$\frac{1+lnx}{x}$(x>0),
记F(x)=-$\frac{1+lnx}{x}$,(x>0),
则F′(x)=$\frac{lnx}{{x}^{2}}$,
所以当x∈(0,1]时,F′(x)≤0,函数单调递减;
当x∈(1,+∞)时,F′(x)>0,函数单调递增,
故F(x)≥F(1)=-1,即F(x)的最小值为-1,
故c≤-1.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,是一道中档题.

| A. | -$\frac{24}{25}$ | B. | -$\frac{16}{25}$ | C. | $\frac{24}{25}$ | D. | $\frac{12}{25}$ |
| A. | -3 | B. | 3 | C. | -1 | D. | 1 |
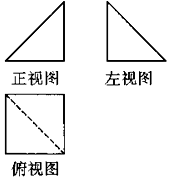 如图,一个多面体的正视图和侧视图是两个全等的等腰直角三角形且直角边长为2,俯视图是边长为2的正方形,则该多面体的最大面的面积是( )
如图,一个多面体的正视图和侧视图是两个全等的等腰直角三角形且直角边长为2,俯视图是边长为2的正方形,则该多面体的最大面的面积是( )| A. | 2 | B. | $4\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | sinθ>0 | B. | cosθ>0 | C. | tanθ>0 | D. | 以上都不对 |