题目内容
7.设Sn是等比数列{an}的前n项和,an>0,若S6-2S3=5,则S9-S6的最小值为20.分析 利用等比数列的前n项和公式、数列的单调性、基本不等式的性质即可得出.
解答 解:设等比数列{an}的公比q>0,q≠1.
∵S6-2S3=5,
∴$\frac{{a}_{1}({q}^{6}-1)}{q-1}$-$\frac{2{a}_{1}({q}^{3}-1)}{q-1}$=5.
∴$\frac{{a}_{1}({q}^{3}-1)^{2}}{q-1}$=5.∴q>1.
则S9-S6=$\frac{{a}_{1}({q}^{9}-1)}{q-1}$-$\frac{{a}_{1}({q}^{6}-1)}{q-1}$=$\frac{{a}_{1}({q}^{3}-1)}{q-1}$•q6=$\frac{5{q}^{6}}{{q}^{3}-1}$=5$[({q}^{3}-1)+\frac{1}{{q}^{3}-1}]$+10≥5×$2\sqrt{({q}^{3}-1)•\frac{1}{{q}^{3}-1}}$+10=20,当且仅当q3=2,即q=$\root{3}{2}$时取等号.
∴S9-S6的最小值为20.
故答案为:20.
点评 本题考查了等比数列的前n项和公式、数列的单调性、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
12.函数y=ln(ax2+x-1)的值域为R,当且仅当( )
| A. | a≥0 | B. | a>0 | C. | a$≥-\frac{1}{4}$ | D. | a$<-\frac{1}{4}$ |
2.已知a>0,函数f(x)=eaxsinx(x∈[0,+∞)).记xn为f(x)的从小到大的第n(n∈N*)个极值点,则数列{f(xn)}是( )
| A. | 等差数列,公差为eax | B. | 等差数列,公差为-eax | ||
| C. | 等比数列,公比为eax | D. | 等比数列,公比为-eax |
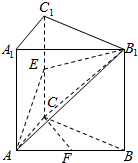 如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,AC=BC=1,AA1=2.
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,AC=BC=1,AA1=2.