题目内容
20.执行如图所示的程序框图,若输入S的值为$\frac{1}{2}$,则输出S的值为( )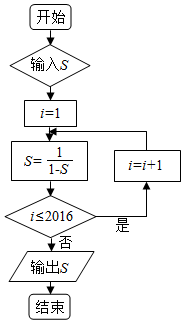
| A. | -1 | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
分析 模拟程序框图的运行过程,得出执行程序中S的值是以3为周期的函数,分析循环条件,求出程序运行后输出的S值.
解答 解:输入S=$\frac{1}{2}$时,执行程序如下:
i=1,S=2,
i=2,满足进行循环的条件,S=-1,
i=3,满足进行循环的条件,S=$\frac{1}{2}$,
i=4,满足进行循环的条件,S=2;…,
i=2016=672×3,满足进行循环的条件,S=$\frac{1}{2}$;
当i=2017时,不满足进行循环的条件;
输出S值为$\frac{1}{2}$,
可以把2016看成3,可知当i=4时输出s为2;即可得出结论.
故选:B.
点评 本题考查了程序框图的应用问题,解题时应模拟程序运行的过程,是基础题目.

练习册系列答案
相关题目
10.已知直线l和平面α,若l∥α,P∈α,则过点P且垂直于l的直线( )
| A. | 只有一条,不在平面α内 | B. | 只有一条,且在平面α内 | ||
| C. | 有无数条,一定在平面α内 | D. | 有无数条,不一定在平面α内 |
8.一个物体的运动方程是s=3tcost+x(x为常数),则其速度方程为( )
| A. | v=3cost-3tsint+1 | B. | v=3cost-3tsint | ||
| C. | v=-3sint | D. | v=3cost+3tsint |
15.若圆${C_1}:{(x-1)^2}+{y^2}=1$与圆${C_2}:{x^2}+{y^2}-8x-8y+m=0$相交,则m的取值范围为( )
| A. | (-2,8) | B. | (-∞,-2)∪(8,+∞) | C. | (-4,16) | D. | (-∞,-4)∪(16,+∞) |
5.已知函数f(x)=$\frac{x}{x+1}$+2x-mln(x+1)在(0,+∞)上是增函数,则实数m的取值范围为( )
| A. | (-∞,2$\sqrt{2}$] | B. | (-∞,2$\sqrt{2}$) | C. | (-∞,3) | D. | (-∞,3] |
9.若复数z满足$\frac{z}{(1+i)^{2}}$=cos60°+isin60°,其中i为虚数单位,则z=( )
| A. | -$\sqrt{3}$-i | B. | -$\sqrt{3}$+i | C. | 1+$\sqrt{3}$i | D. | 1-$\sqrt{3}$i |
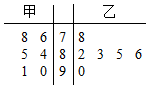 吉安市某校的甲乙两名同学在6次数学竞赛辅导测试中的成绩统计如图的茎叶图所示:
吉安市某校的甲乙两名同学在6次数学竞赛辅导测试中的成绩统计如图的茎叶图所示: