题目内容
7.已知函数f(x)=x3+sinx,x∈(-1,1).如果f(1-a)+f(1-a2)<0,则a的取值范围是( )| A. | $(1,\sqrt{2})$ | B. | (-∞,-2)∪(1,+∞) | C. | (-∞,-1)∪(2,+∞) | D. | $(0,\sqrt{2})$ |
分析 根据条件判断函数f(x)的奇偶性和单调性即可.
解答 解:∵f(x)=sinx+x3,
∴f(-x)=-f(x),即函数f(x)是奇函数,
函数的导数f′(x)=cosx+3x2>0,
则函数f(x)在x∈(-1,1)上为增函数,
则不等式f(1-a)+f(1-a2)<0,
等价为f(1-a)<-f(1-a2)=f(a2-1),
即$\left\{\begin{array}{l}{-1<1-a<1}\\{-1{<a}^{2}-1<1}\\{1-a{<a}^{2}-1}\end{array}\right.$,解得:1<a<$\sqrt{2}$,
故选:A.
点评 本题主要考查不等式的求解,根据条件判断函数的奇偶性和单调性是解决本题的关键.综合考查函数的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.一离散型随机变量X的概率分布列为
且E(X)=1.5,则a-b=0.
| X | 0 | 1 | 2 | 3 |
| P | 0.1 | a | b | 0.1 |
12.集合A={$\frac{9}{10-x$∈N|x∈N}的真子集的个数是( )
| A. | 4 | B. | 7 | C. | 8 | D. | 16 |
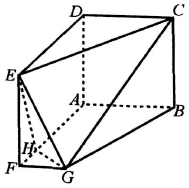 在多面体ABCDEFG中,四边形ABCD与ADEF是边长均为a的正方形,四边形ABGH是直角梯形,AB⊥AF,且FA=2FG=4FH.
在多面体ABCDEFG中,四边形ABCD与ADEF是边长均为a的正方形,四边形ABGH是直角梯形,AB⊥AF,且FA=2FG=4FH.