题目内容
求值：sin10°cos20°sin30°cos40°…cos80°sin90°．
考点：二倍角的正弦,同角三角函数基本关系的运用
专题：三角函数的求值
分析：原式先利用特殊角的三角函数值计算，结合后，利用二倍角的正弦函数公式化简，整理即可求出值．
解答：
解：∵sin10°sin50°sin70°=cos20°cos40°cos80°=
=
=
=
=
，
∴则原式=（cos20°cos40°cos60°cos80°）•（sin10°sin30°sin50°sin70°sin90°）
=
（cos20°cos40°cos80°）•（sin10°sin50°sin70°）
=
．
| sin20°cos20°cos40°cos80° |
| sin20° |
| ||
| sin20° |
| ||
| sin20° |
| ||
| sin20° |
| 1 |
| 8 |
∴则原式=（cos20°cos40°cos60°cos80°）•（sin10°sin30°sin50°sin70°sin90°）
=
| 1 |
| 4 |
=
| 1 |
| 256 |
点评：此题考查了同角三角函数基本关系的运用，二倍角的正弦函数公式，以及诱导公式的作用，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
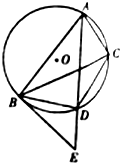如图，A，B，C为⊙O上的三个点，AD是∠BAC的平分线，交⊙O于点D，过B作⊙O的切线交Ad的延长线于点E．