题目内容
在等比数列{an}中,a1=4,q=5,则使Sn>107成立的最小n的值是 .
考点:数列与不等式的综合
专题:等差数列与等比数列
分析:直接由已知写出等比数列的前n项和,代入Sn>107求得最小自然数n的值.
解答:
解:在等比数列中,由a1=4,q=5,
得Sn=
=5n-1,代入Sn>107,得
5n-1>107,解得:n>log5(107+1).
∵10<log5(107+1)<11,
∵n∈N,∴n≥11.
即满足Sn>107的最小自然数是11.
故答案为:11.
得Sn=
| 4(1-5n) |
| 1-5 |
5n-1>107,解得:n>log5(107+1).
∵10<log5(107+1)<11,
∵n∈N,∴n≥11.
即满足Sn>107的最小自然数是11.
故答案为:11.
点评:本题考查了等比数列的前n项和,考查了指数不等式的解法,是中档题.

练习册系列答案
相关题目
在同一平面直角坐标系中,已知函数y=f(x)的图象与y=ex的图象关于直线y=x对称,则函数y=f(x)-x的单调增区间为( )
| A、(-∞,1] |
| B、(0,+∞) |
| C、[1,+∞) |
| D、(0,1] |
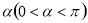 的大小。
的大小。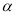 所在的扇形弧长
所在的扇形弧长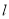 及弧所在的弓形的面积S。
及弧所在的弓形的面积S。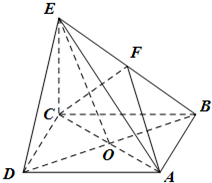 在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥平面ABCD,F为BE的中点.
在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥平面ABCD,F为BE的中点. 如图,在三棱锥P-ABC中,AB=5,BC=4,AC=3,点D是线段PB的中点,平面PAC⊥平面ABC.
如图,在三棱锥P-ABC中,AB=5,BC=4,AC=3,点D是线段PB的中点,平面PAC⊥平面ABC.