题目内容
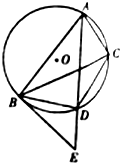如图，A，B，C为⊙O上的三个点，AD是∠BAC的平分线，交⊙O于点D，过B作⊙O的切线交Ad的延长线于点E．（Ⅰ）证明：BD平分∠EBC；
（Ⅱ）证明：AE•DC=AB•BE．
考点：相似三角形的判定,与圆有关的比例线段
专题：计算题,直线与圆
分析：（1）由BE是⊙O的切线，可得∠EBD=∠BAD，又∠CBD=∠CAD，∠BAD=∠CAD，从而可求∠EBD=∠CBD，即可得解．
（2）先证明△BDE∽△ABE，可得
=
，又可求∠BCD=∠DBC，BD=CD，从而可得
=
=
，即可得解．
（2）先证明△BDE∽△ABE，可得
| BE |
| AE |
| BD |
| AB |
| BE |
| AE |
| BD |
| AB |
| CD |
| AB |
解答：
解：（1）因为BE是⊙O的切线，所以∠EBD=∠BAD…（2分）
又因为∠CBD=∠CAD，∠BAD=∠CAD…（4分）
所以∠EBD=∠CBD，即BD平分∠EBC．…（5分）
（2）由（1）可知∠EBD=∠BAD，且∠BED=∠BED，有△BDE∽△ABE，所以
=
，…（7分）
又因为∠BCD=∠BAE=∠DBE=∠DBC，所以∠BCD=∠DBC，BD=CD…（8分）
所以
=
=
，…（9分）
所以AE•DC=AB•BE…（10分）
解：（1）因为BE是⊙O的切线，所以∠EBD=∠BAD…（2分）又因为∠CBD=∠CAD，∠BAD=∠CAD…（4分）
所以∠EBD=∠CBD，即BD平分∠EBC．…（5分）
（2）由（1）可知∠EBD=∠BAD，且∠BED=∠BED，有△BDE∽△ABE，所以
| BE |
| AE |
| BD |
| AB |
又因为∠BCD=∠BAE=∠DBE=∠DBC，所以∠BCD=∠DBC，BD=CD…（8分）
所以
| BE |
| AE |
| BD |
| AB |
| CD |
| AB |
所以AE•DC=AB•BE…（10分）
点评：本题主要考查了相似三角形的判定，与圆有关的比例线段的应用，解题时要认真审题，注意圆的切线的性质的灵活运用，属于中档题．
练习册系列答案
相关题目
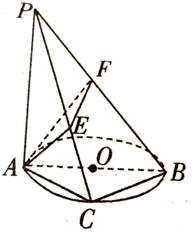如图，AB是圆O的直径，C为圆周上一点，PA⊥平面ABC，若AE⊥PC，F是PD上任意一点，求证：平面AEF⊥平面PBC．
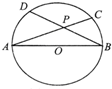如图，AB是圆O的直径，过A、B的两条弦AC和BD相交于点P，若圆O的半径是3，则AC•AP+BD•BP的值