题目内容
某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共100个,生产一个卫兵需5min,生产一个骑兵需7min,生产一个伞兵需4min,已知总生产时间不超过10h.若生产一个卫兵可获利润5元,生产一个骑兵可获利润6元,生产一个伞兵可获利润3元.
(1)用每天生产的卫兵个数x与骑兵个数y表示每天的利润W(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
(1)依题意每天生产的伞兵个数为100-x-y,
所以利润W=5x+6y+3(100-x-y)=2x+3y+300.
(2)约束条件为:
目标函数为W=2x+3y+300,
如图所示,作出可行域.

初始直线l0:2x+3y=0,平移初始直线经过点A时,W有最大值,
由
最优解为A(50,50),所以Wmax=550(元).
答:每天生产卫兵50个,骑兵50个,伞兵0个时利润最大,为550元.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案
相关题目
 ,
,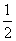 ),则不等式-cx2+2x-a>0的解集为________.
),则不等式-cx2+2x-a>0的解集为________. 所表示的平面区域为S,若A、B为区域S内的两个动点,则|AB|的最大值为( )
所表示的平面区域为S,若A、B为区域S内的两个动点,则|AB|的最大值为( ) B.
B. C.3 D.
C.3 D. 的最大值为( )
的最大值为( )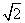 B.2
B.2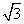 D.2
D.2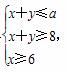 且不等式x+2y≤14恒成立,则实数a的取值范围是( )
且不等式x+2y≤14恒成立,则实数a的取值范围是( ) ) B.(0,
) B.(0,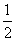 ,1) D.(0,1]
,1) D.(0,1]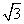 ),那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是________.
),那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是________.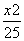 +
+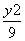 =1上一点M到焦点F1的距离为2,N是MF1的中点,则|ON|等于( )
=1上一点M到焦点F1的距离为2,N是MF1的中点,则|ON|等于( )