题目内容
3.互不相同的5盆菊花,其中2盆为白色,2盆为黄色,1盆为红色,先要摆成一排,要求红色菊花摆放在正中间,白色菊花不相邻,黄色菊花也不相邻,共有多少种摆放方法( )| A. | $A_5^5$ | B. | $A_2^2$ | ||
| C. | $A_4^2A_2^2$ | D. | $C_2^1C_2^1A_2^2A_2^2$ |
分析 由红色菊花摆放在正中间,白色菊花不相邻,黄色菊花也不相邻,则白色菊花不相邻,黄色菊也不相邻,即红菊花两边各一盆白色,黄色菊花,根据分步计数原理可得.
解答 解:由红色菊花摆放在正中间,白色菊花不相邻,黄色菊花也不相邻,则白色菊花不相邻,黄色菊也不相邻,即红菊花两边各一盆白色,黄色菊花,故有$C_2^1C_2^1A_2^2A_2^2$.
故选:D.
点评 本题主要考查排列组合、两个基本原理的实际应用,注意不相邻问题用插空法,属于中档题.

练习册系列答案
相关题目
8.设α∈(0,$\frac{π}{2}$),sinα=$\frac{\sqrt{6}}{3}$,则tanα等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
13.若{an}为等差数列,且a12+a42=3,则a3的最大值为( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{5}{3}$ | D. | $\frac{\sqrt{15}}{3}$ |
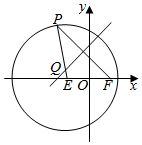 如图,已知圆E:(x+$\sqrt{3}$)2+y2=16,点F($\sqrt{3}$,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
如图,已知圆E:(x+$\sqrt{3}$)2+y2=16,点F($\sqrt{3}$,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.