题目内容
15.已知函数f(x)=ax3-3x2+4,若f(x)存在唯一的零点x0,且x0>0,则实数a的取值范围为a<-1.分析 函数的零点就是对应方程的根,先判断当a=0时对应方程根的个数,再讨论当a不等于0时的根的情况,此时只需利用导数研究该函数的极值,利用极值的符号解决问题.
解答 解:原函数的零点即为ax3-3x2+4=0的根.
当a=0时,原方程化为3x2-4=0,解得$x=±\frac{2}{\sqrt{3}}$,不符合题意,故a≠0;
当a≠0时,f′(x)=3ax2-6x,令f′(x)=0,解得x=0或x=$\frac{2}{a}$.
①若a>0,则x=0是极大值点,x=$\frac{2}{a}$是极小值点,此时若函数只有一个正的零点,则必有f(0)=4<0,显然不成立;
②若a<0,则x=0是极大值点,此时若函数只有一个正的零点,只需f(0)=4>0,且$f(\frac{2}{a})=a•\frac{8}{{a}^{3}}-3•\frac{4}{{a}^{2}}+4>0$,
解得a<-1.
综上可知,a<-1即为所求.
故答案为a<-1.
点评 函数的零点即为对应方程的根,也是函数的图象与x轴交点的横坐标,依此可以将问题适当的进行转化,即此问题最终转化为函数图象与x轴交点的横坐标,通过研究单调性、极值的符号解决问题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
20.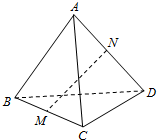 如图,在四面体ABCD,AB=CD,M,N分别是BC,AD的中点,若AB与CD所成的角的大小为60°,则MN和CD所成的角的大小为( )
如图,在四面体ABCD,AB=CD,M,N分别是BC,AD的中点,若AB与CD所成的角的大小为60°,则MN和CD所成的角的大小为( )
 如图,在四面体ABCD,AB=CD,M,N分别是BC,AD的中点,若AB与CD所成的角的大小为60°,则MN和CD所成的角的大小为( )
如图,在四面体ABCD,AB=CD,M,N分别是BC,AD的中点,若AB与CD所成的角的大小为60°,则MN和CD所成的角的大小为( )| A. | 30° | B. | 60° | C. | 30°或60° | D. | 15°或60° |