题目内容
9.已知3A${\;}_{x}^{3}$=$2{A}_{x+1}^{2}$$+6{A}_{x}^{2}$,则x等于( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 根据排列数的公式,化简方程,求出方程的解即可.
解答 解:∵3A${\;}_{x}^{3}$=$2{A}_{x+1}^{2}$$+6{A}_{x}^{2}$,
∴3•x(x-1)(x-2)=2•x(x+1)+6•x(x-1),
化简得3x2-17x+10=0,
解得x=5或x=$\frac{2}{3}$(不合题意,舍去),
∴x=5.
故选:A.
点评 本题考查了排列数的公式与应用问题,也考查了解一元二次方程的问题,是基础题目.

练习册系列答案
相关题目
19.已知向量$\overrightarrow a=(x,-1)$,$\overrightarrow b=(x,4)$,其中x∈R.则“x=2”是“$\overrightarrow a⊥\overrightarrow b$”成立的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
20.设向量$\overrightarrow{a}$=(2,-1),$\overrightarrow{b}$=(x,3)且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则x=( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 3 | D. | -2 |
 (
(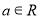 ).
). 时,讨论函数
时,讨论函数 的单调性;
的单调性; ,当
,当 时,若对任意
时,若对任意 ,存在
,存在 ,使
,使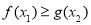 ,求实数
,求实数 的取值范围.
的取值范围.