题目内容
1.在△ABC中,若a2+b2=c2+ab,且a+b=20,求△ABC周长的最小值和面积的最大值,并指出此时三角形的形状.分析 由条件利用余弦定理求得C=$\frac{π}{3}$,再利用基本不等式求得ab的最大值以及c的最小值,可得△ABC周长的最小值和面积的最大值,根据等号成立条件求得此时三角形的形状.
解答 解:△ABC中,若a2+b2=c2+ab,则cosC=$\frac{{a}^{2}{+b}^{2}{-c}^{2}}{2ab}$=$\frac{1}{2}$,∴C=$\frac{π}{3}$.
∵a+b=20≥2$\sqrt{ab}$,∴ab≤100,当且仅当 a=b时,取等号,
∴c=$\sqrt{{a}^{2}{+b}^{2}-2ab•cosC}$=$\sqrt{{(a+b)}^{2}-3ab}$=$\sqrt{400-3ab}$≥$\sqrt{400-300}$=10,
故△ABC周长的最小值为a+b+c=20+10=30,
面积的最大值为$\frac{1}{2}$ab•sinC=50•$\frac{\sqrt{3}}{2}$=25$\sqrt{3}$,
此时,△ABC的三边相等,都等于10,△ABC为等边三角形.
点评 本题主要考查余弦定理、基本不等式的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>b>0)与两条平行直线l1:y=x+a与l2:y=x-a相交所得的平行四边形的面积为6b2.则双曲线的离心率是( )
| A. | $\sqrt{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 2 |
10.若$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是两个单位向量,且(2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)•(-2$\overrightarrow{{e}_{1}}$+3$\overrightarrow{{e}_{2}}$)=2$\sqrt{2}$-1,则$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$的夹角为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{2π}{3}$ |
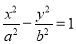 (
(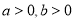 )的左、右焦点分别为
)的左、右焦点分别为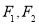 ,且线段
,且线段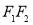 被抛物线
被抛物线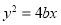 的焦点分成
的焦点分成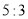 的两段,则双曲线的离心率为( )
的两段,则双曲线的离心率为( )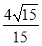 B.
B.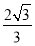 C.
C.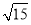 D.
D.